Advertisements
Advertisements
Question
Calculate the percentage efficiency of packing in the case of body centered cubic crystal.
Solution
In body centered cubic arrangement the spheres are touching along the leading diagonal of the cube as shown in the figure.

In ∆ABC
Ac2 = AB2 + BC2
AC = `sqrt("AB"^2 + "BC"^2)`
AC = `sqrt("a"^2 + "a"^2)`
= `sqrt(2"a"^2)`
= `sqrt2"a"`
In ∆ACG
AG2 = AC2 + CG2
AG = `sqrt("AC"^2 + "CG"^2)`
AG = `sqrt((sqrt2"a")^2 + "a"^2)`
AG = `sqrt(2"a"^2 + "a"^2)`
= `sqrt(3"a"^2)`
= `sqrt3"a"`
i.e., `sqrt3"a"` = 4r
r = `sqrt3/4 "a"`
∴ Volume of the sphere with radius ‘r’
= `4/3π"r"^3`
= `4/3π (sqrt3/4 "a")^3`
= `sqrt3/16π "a"^3`
Number of spheres belong to a unit cell in bcc arrangement is equal to two and hence the total volume of all spheres
= `2 xx ((sqrt3π "a"^3)/16)`
= `(sqrt3π "a"^3)/8`
Packing fraction = `"Total volume occupied by spheres in a unit cell"/"Volume of the unit cell" xx 100`
Packing fraction = `(((sqrt3π "a"^3)/8))/(("a"^3)) xx 100`
= `(sqrt3π)/8 xx 100`
= `sqrt3π xx 12.5`
= 1.732 × 3.14 × 12.5
= 68%
i.e., 68 % of the available volume is occupied. The available space is used more efficiently than in simple cubic packing.
APPEARS IN
RELATED QUESTIONS
The ratio of close packed atoms to tetrahedral hole in cubic packing is ____________.
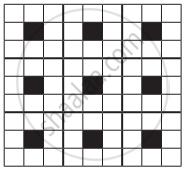
A two-dimensional solid pattern formed by two different atoms X and Y is shown below. The black and white squares represent atoms X and Y respectively. the simplest formula for the compound based on the unit cell from the pattern is
Distinguish between hexagonal close packing and cubic close packing.
Distinguish tetrahedral and octahedral voids.
Explain AAAA and ABABA and ABCABC type of three dimensional packing with the help of neat diagram.
What is the two dimensional coordination number of a molecule in square close packed layer?
