Question

Change the order of integration and evaluate `int_0^1 int_x^sqrt(2-x^2 x  dx  dy)/sqrt(x^2+y^2)`

Answer 1

 Let `int_0^1 int_x^sqrt(2-x^2 x  dx  dy)/sqrt(x^2+y^2)` 

Region of integration is : i)` x<=y<=sqrt(2-x^2)` 

                                        ii)  `0<= x<=1`

                                        iii) `y=sqrt(2-x^2)`  =>                                                               `x^2+y^2=2` 

Circle with centre (0,0) and radius `sqrt2` 

Intersection of circle and y= x line is (1,1) in `1^(st)` quadrant. 

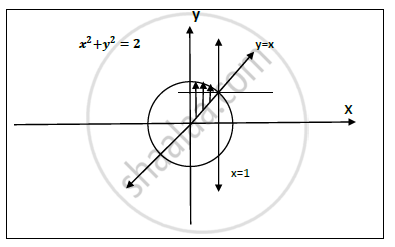
Divide the region into two parts as shown in fig.
After changing the order of integration : 

For one region :   ` 0 <= x <=  y` 

                              `0 <= y <=  1`  

For another region :        `0<=x<= sqrt(2-y^2)` 

                                            `1 <= y <=  sqrt2`   

∴` int_0^1 int_0^y (x   dx  dy)/sqrt(x^2+y^2)` 

= `int_0^1 [sqrt(x^2+y^2)]_0^y dy + int_1^sqrt2 [sqrt(x^2+y^2)]_0^sqrt(2-y^2)`    

=`int_0^1 (sqrt2.y-y) dy + int_1^sqrt2(sqrt2-1) dy`

=` (sqrt2-1) [y^2/2]_0^1+[sqrt2y-y^2/2]sqrt2/1`

=` 1-1/sqrt2`

∴ `I=sqrt(2-1)/sqrt2`