Advertisements
Advertisements
Question
Change to polar coordinates and evaluate `int_0^1 int_0^x (x+y)dydx`
Solution
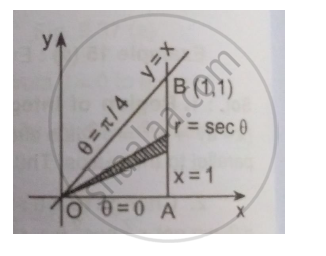
1) Region of integration: y= 0 is the x-axis and y = x is a line OB through the origin; x = 0 is the y-axis and x = 1 is a line AB parallel to the y-axis. Thus the region of integration is the triangle OAB.
2) Change to r, θ: Putting x = r cos θ and y = r sin θ, the line y = x becomes r sin θ= r cos θ i.e. tan θ = 1 i.e. θ =`pi/4`. The x-axis is given by θ = 0 and the y-axis is given by θ =`pi/2`. And line x = 1 is given by r cos θ = 1 i.e. r = sec θ.
3) Integrand: Putting x = r cos θ and y = r sin θ in (x + y), we get, r cos θ + r sin θ = r(cos θ + sin θ) and dydx is replaced by r drdθ
∴ `I=int_0^(pi/4) int_0^secθ r(cos θ+sin θ )rdr dθ`
`I= int_0^(pi/4) int_0^secθ (cosθ+sinθ)r^2 dr dθ`
`I= int_0^(pi/4) (cos θ+sinθ) [r^3/3]_0^secθ dθ`
`I=1/3int_0^(pi/4) (cos θ+ sin θ) sec^3 θ dθ`
`I=1/3[int_0^(pi/4) sec^2 θ dθ +int_0^(pi/4) 1/cos^3 θ sinθ dθ]`
`I=1/3 [tan θ+1/(2cos^2θ)]_0^(pi/4)`
`I=1/3 (1+1/2 (2-1))`
`I=1/2`
