Advertisements
Advertisements
Question
चौकोन ABCD मध्ये बाजू AD || BC, कर्ण AC आणि BD परस्परांना P बिंदूत छेदतात, तर सिद्ध करा, की `"AP"/"PD" = "PC"/"BP".`
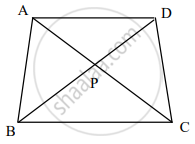
Solution
रेख AD || रेख BC व
BD ही त्यांची छेदिका आहे. .......[पक्ष]
∴ ∠DBC ≅ ∠BDA .............[व्युत्क्रम कोन]
∴ ∠PBC ≅ ∠PDA …(i)[D−P−B]
∆PBC व ∆PDA मध्ये,
∠PBC ≅ ∠PDA ... [(i) वरून]
∠BPC ≅ ∠DPA ..........[विरुद्ध कोन]
∴ ∆PBC ∼ ∆PDA ...............[समरूपतेची कोको कसोटी]
∴ `"BP"/"PD" = "PC"/"AP"` .............[समरूप त्रिकोणांच्या संगत बाजू]
∴ `"AP"/"PD" = "PC"/"BP"` .............[एकांतर क्रिया]
APPEARS IN
RELATED QUESTIONS
Δ ABC मध्ये AP ⊥ BC, BQ ⊥ AC B-P-C, A-Q-C तर, Δ CPA ∼ Δ CQB दाखवा. जर AP = 7, BQ = 8, BC = 12 तर AC काढा.

आकृतीत रेख AC व रेख BD परस्परांना P बिंदूत छेदतात आणि `"AP"/"CP" = "BP"/"DP"` तर सिद्ध करा, ΔABP ∼ ΔCDP.
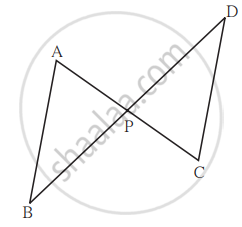
आकृती मध्ये रेख PQ || रेख DE, A (Δ PQF) = 20 एकक, जर PF = 2 DP आहे, तर A(`square"DPQE"`) काढण्यासाठी खालील कृती पूर्ण करा.
A(Δ PQF) = 20 एकक, PF = 2 DP, DP = x मानू. ∴ PF = 2x
DF = DP + `square` = `square` + `square` = 3x
Δ FDE व Δ FPQ मध्ये
∠ FDE ≅ ∠`square` (संगत कोन)
∠ FED ≅ ∠`square` (संगत कोन)
∴ Δ FDE ∼ Δ FPQ .............(कोको कसोटी)
∴ `("A"(Δ"FDE"))/("A"(Δ"FPQ")) = square/square = ((3"x")^2)/((2"x")^2) = 9/4`
A(Δ FDE) = `9/4` × A(Δ FPQ ) = `9/4 xx square = square`
A(`square` DPQE) = A(Δ FDE) - A(Δ FPQ)
= `square - square`
= `square`
जर ΔABC व ΔPQR मध्ये एका एकास एक संगतीत `"AB"/"QR" = "BC"/"PR" = "CA"/"PQ"` तर खालीलपैकी सत्य विधान कोणते?

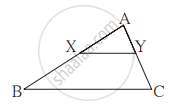
आकृती मध्ये रेख XY || रेख BC तर खालील पैकी कोणते विधान सत्य आहे?
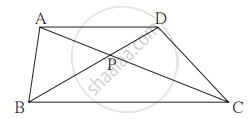
`square`ABCD मध्ये रेख AD || रेख BC. कर्ण AC आणि कर्ण BD परस्परांना बिंदू P मध्ये छेदतात. तर दाखवा की `"AP"/"PD" = "PC"/"BP"`
खालीलपैकी कोणती कसोटी समरूपतेची नाही?
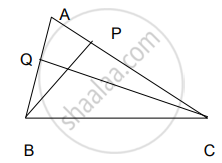
शेजारील आकृतीमध्ये, BP लंब AC, CQ लंब AB, A-P-C आणि A-Q-B, तर ∆APB व ∆AQC समरूप दाखवा.
∆APB व ∆AQC मध्ये,
∠APB = `square^circ` ......(i)
∠AQC = `square^circ` ......(ii)
∠APB ≅ ∠AQC …[(i) व (ii) वरून]
∠PAB ≅ ∠QAC .............` square`
∆APB ~ ∆AQC .............` square`
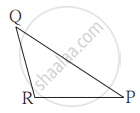
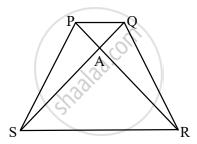
आकृतीमध्ये समलंब चौकोन PQRS मध्ये बाजू PQ || बाजू SR, AR = 5 AP, तर सिद्ध करा, SR = 5 PQ.
आकृतीमध्ये त्रिकोण ABC मध्ये बाजू BC वर D हा बिंदू असा आहे, की ∠BAC = ∠ADC. तर सिद्ध करा, की CA2 = CB × CD.