Question

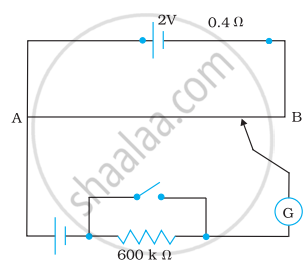
चित्र में एक पोटेशियोमीटर दर्शाया गया है। जिसमें एक 2.0 V और आन्तरिक प्रतिरोध 0.40 Ω का कोई सेल, पोटेशियोमीटर के प्रतिरोधक तार AB पर वोल्टता पात बनाए A रखता है। कोई मानक सेल जो 1.02 V का अचर विद्युत वाहक बल बनाए रखता है (कुछ mA की बहुत सामान्य धाराओं के लिए) तार की 67.3 cm लम्बाई पर सन्तुलन बिन्दु देता है। मानक सेल से अति न्यून धारा लेना सुनिश्चित करने के लिए । इसके साथ परिपथ में श्रेणी 600 kΩ का एक अति उच्च प्रतिरोध इसके साथ सम्बद्ध किया जाता है, जिसे सन्तुलन बिन्दु प्राप्त होने के निकट लघुपथित (shorted) कर दिया जाता है। इसके बाद मानक सेल को किसी अज्ञात विद्युत वाहक बल E के सेल से प्रतिस्थापित कर दिया जाता है जिससे सन्तुलन बिन्द तार की 82.3 cm लम्बाई पर प्राप्त होता है।

1. E का मान क्या है?
2. 600 kΩ के उच्च प्रतिरोध का क्या प्रयोजन है?
3. क्या इस उच्च प्रतिरोध से सन्तुलन बिन्दु प्रभावित होता है?
4. क्या परिचालक सेल के आन्तरिक प्रतिरोध से सन्तुलन बिन्दु प्रभावित होता है?
5. उपर्युक्त स्थिति में यदि पोटेशियोमीटर के परिचालक सेल का विद्युत वाहक बल 2.0 V के स्थान पर 1.0 V हो तो क्या यह विधि फिर भी सफल रहेगी?
6. क्या यह परिपथ कुछ mV की कोटि के अत्यल्प विद्युत वाहक बलों (जैसे कि किसी प्रारूपी तापविद्युत युग्म का विद्युत वाहक बल) के निर्धारण में सफल होगी? यदि नहीं, तो आप इसमें किस प्रकार संशोधन करेंगे?

Answer 1

(a) विभवमापी के तार की समान विभव प्रवणता के लिए, दो सेलों के वै० वा० बलों की तुलना करने का सूत्र निम्न है।

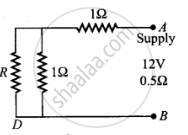
माना बिन्दुओं A व B के बीच तुल्य प्रतिरोध R है।

चूँकि अनन्त `+- 1` = अनन्त,

अतः बिन्दुओं C व D के बीच प्रतिरोध वही होगा जो बिन्दुओं A व B के बीच है; अतः समान्तरक्रम में जुड़े प्रतिरोध R तथा 1 Ω का तुल्य प्रतिरोध,

`"R"_1 = ("R" xx 1)/("R" + 1) = "R"/("R" + 1)`

बिन्दुओं A व B के बीच तुल्य प्रतिरोध

R_AB = R₁ + 1 + 1

अतः परिकल्पना से R₁ + 1 + 1 = R

`=> "R"/("R + 1") + 2 = "R"`

⇒ R + 2(R + 1) = R(R + 1)

⇒ 3R + 2 = R² + R

⇒ R² - 2R - 2 = 0

⇒ R = `(2+- sqrt(4 + 4 xx 2))/2 = (2 +- sqrt 12)/2 = 1 +- sqrt3  Omega`

चूँकि प्रतिरोध ऋणात्मक नहीं हो सकता

∴ R = `(1 + sqrt3)Omega = (1 + 1.732)Omega = 2.732 Omega`

सप्लाई से ली गयी धारा, I = `12/("R + r")`

`= 12/(2.732 + 0.5) = 12/(3.232 " A")`

= 3.7 A

(b) उच्च प्रतिरोध का प्रयोजन धारामापी में धारा को कम करना है जबकि जौकी संतुलन बिन्दु से दूर है। इससे प्रमाणिक सेल नुकसान (damage) से बचा रहता है।

(c) संतुलन बिन्दु उच्च प्रतिरोध से प्रभावित नहीं होता है, क्योंकि संतुलन की स्थिति में सेल के द्वितीयक परिपथ में धारा नहीं बहती।

(d) परिचालक सेल के आन्तरिक प्रतिरोध से संतुलन बिन्दु प्रभावित नहीं होता क्योंकि हमने तार पर विभव प्रवणता पहले से ही नियत रख दी है।

(e) नहीं, क्योंकि विभवमापी के कार्य करने के लिए परिचालक सेल का वै० वी० बल, द्वितीयक परिपथ के सेल के वै० वा० बल

(E) से अधिक होना चाहिए।

(f) क्योकि संतुलन बिन्दु सिरे A के निकट होगा तथा मापन में त्रुटि बहुत अधिक होगी। इसके लिए परिचालक सेल के श्रेणीक्रम में एक परिवर्ती प्रतिरोध (R) जोड़ते हैं तथा इसका मान इस प्रकार व्यवस्थित करते हैं कि तार AB के सिरों के बीच विभवपात द्वितीयक सेल के वै० वा० बल से थोड़ा ही अधिक हो ताकि संतुलन बिन्दु अधिक लम्बाई पर प्राप्त हो, इससे मापन में त्रुटि कम होगी तथा मापने की यथार्थता बढ़ेगी।