Advertisements
Advertisements
Question
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: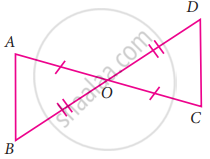
Solution
In the given figure AC and BD bisect each other at O.
∴ OA = OC ...(Given), OB = OD ...(Given)
∠AOB = ∠COD ...(vertically opposite angles)
By SAS congruency
ΔAOB ≅ ΔOCD
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 7 cm, BC = 5 cm, ∠B = 50°.
∆DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°.
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 4.5 cm, AC = 4 cm, ∠A = 60°.
∆DEF, DE = 4 cm, FD = 4.5 cm, ∠D = 55°.
Construct a triangle PQR with given conditions.
∠Q = 90°, ∠R = 42° and QR = 5.5 cm
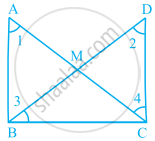
In the given figure, M is the mid-point of both AC and BD. Then ______.
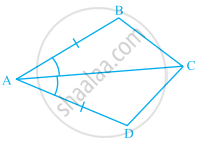
In the given figure, AB = AD and ∠BAC = ∠DAC. Then
- ∆ ______ ≅ ∆ABC.
- BC = ______.
- ∠BCA = ______.
- Line segment AC bisects ______ and ______.
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
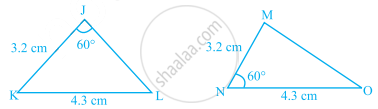
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
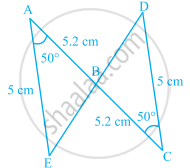
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
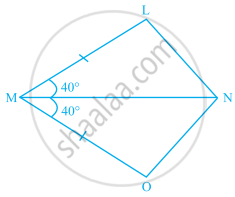
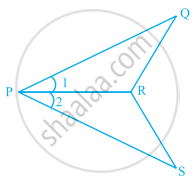
In the given figure, PO = PS and ∠1 = ∠2.
- Is ∆PQR ≅ ∆PSR? Give reasons.
- Is QR = SR? Give reasons.