Advertisements
Advertisements
Question
Construct a triangle whose sides are 3.6 cm, 3.0 cm and 4.8 cm. Bisect the smallest angle and measure each part.
Solution
Step 1: Draw a Ray BX and with B as center and radius 4.8 cm cut an arc on the line and name it as C.
Step 2: With B as center and 3.6 cm as radius draw an arc.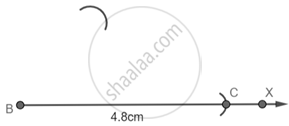
Step 3: With C as center and 3 cm as radius cut the previous arc at A.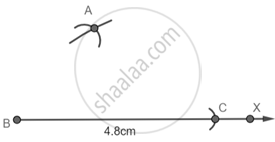
Step 4: Join AB and AC.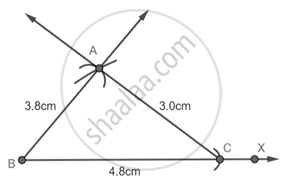
Our triangle is constructed.
Now we know that the angle opposite to the smallest side is the smallest angle in a triangle.
So ∠ABC is the smallest.
Now bisecting the ∠ABC
Step 5: With B as center draw an arc that cuts AB and BC at P and Q respectively.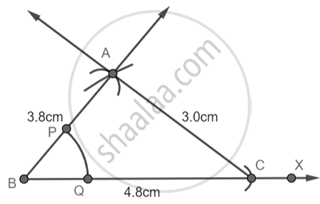
Step 6: With P as center and radius more than PQ draw an arc then with Q as center and equal radius draw another arc that cuts the previous arc at Z.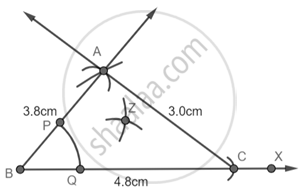
Step 7: Join BZ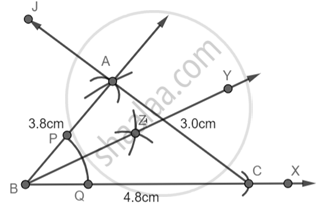
Now by cosine rule, we get to know that ∠ABC = 40°
So, ∠ABY = ∠YBC = 20°.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB − AC = 3.5 cm.
Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR − PQ = 2 cm
Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Construct a ΔABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
The construction of a triangle ABC, given that BC = 3 cm, ∠C = 60° is possible when difference of AB and AC is equal to ______.
An angle of 52.5° can be constructed.
A triangle ABC can be constructed in which AB = 5 cm, ∠A = 45° and BC + AC = 5 cm.
Construct the following and give justification:
An equilateral triangle if its altitude is 3.2 cm.
