Advertisements
Advertisements
Question
Construct the following and give justification:
An equilateral triangle if its altitude is 3.2 cm.
Solution
Step 1: Draw a line XY.
Step 2: Mark a point D on XY and construct DZ perpendicular to XY.
Step 3: With center D and radius 3.2 cm cut an arc on DZ at A.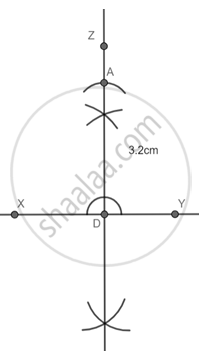
Step 4: With A as center, draw ∠UAD = 30° intersecting XY at B and ∠VAD = 30° intersecting XY at C.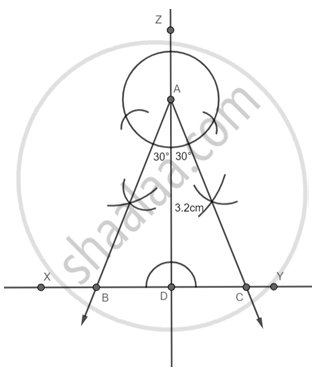
ABC is the required triangle.
Justification:
By construction we can say,
∠ZDY = 90°
∠BAC = ∠BAD + ∠CAD
∠BAC = 30° + 30° = 60°
In ΔABD,
∠ABD + ∠BAD + ∠DBA = 180° ...(By angle sum property)
30° + 90° + ∠DBA = 180°
∠DBA = 60°
Similary, ∠DCA = 60°
Thus, ∠A = ∠B = ∠C = 60°
Thus, our construction is justified.
APPEARS IN
RELATED QUESTIONS
Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR − PQ = 2 cm
Construct a ΔABC in which AB + AC = 5.6 cm, BC = 4.5 cm, AB − AC = 1.5 cm and ∠B = 45°.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45° .
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Construct a triangle ABC such that BC = 6 cm, AB = 6 cm and median AD = 4 cm.
An angle of 52.5° can be constructed.
An angle of 42.5° can be constructed.
Construct the following and give justification:
A right triangle when one side is 3.5 cm and sum of other sides and the hypotenuse is 5.5 cm.
Construct the following and give justification:
A rhombus whose diagonals are 4 cm and 6 cm in lengths.
