Advertisements
Advertisements
Question
Construct the following and give justification:
A right triangle when one side is 3.5 cm and sum of other sides and the hypotenuse is 5.5 cm.
Solution
In the right triangle ABC, given BC = 3.5 cm, ∠B = 90° and sum of other side and hypotenuse be, AB + AC = 5.5 cm
To construct a triangle ABC use the following steps:
1. Draw the base BC = 3.5 cm
2. Make an angle XBC = 90° at the point B of base BC.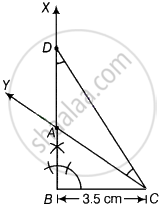
3. Cut the line segment BD equal to AB + AC i.e., 5.5 cm from the ray XB.
4. Join DC and make an ∠DCY equal to ∠BDC.
5. Let Y intersect BX at A. Therefore, ABC is the required triangle.
Justification:
Base BC and ∠B are drawn as given.
In ΔACD, ∠ACD = ∠ADC ...[By construction]
AD = AC ...(i) [Sides opposite to equal angles are equal]
Now, AB = BD – AD = BD – AC ...[From equation (i)]
BD = AB + AC
Hence, our construction is justified.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB − AC = 3.5 cm.
Construct a ΔABC in which BC = 3.4 cm, AB − AC = 1.5 cm and ∠B = 45°.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45° .
Using ruler and compasses only, construct a ΔABC from the following data:
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60°.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Construct a triangle ABC such that BC = 6 cm, AB = 6 cm and median AD = 4 cm.
The construction of a triangle ABC, given that BC = 6 cm, ∠B = 45° is not possible when difference of AB and AC is equal to ______.
A triangle ABC can be constructed in which ∠B = 60°, ∠C = 45° and AB + BC + AC = 12 cm.
Construct a triangle ABC in which BC = 5 cm, ∠B = 60° and AC + AB = 7.5 cm.
