Question

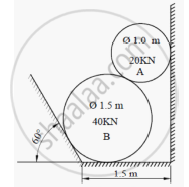
Cylinder A (diameter 1m, weight 20 kN) and cylinder B (diameter 1.5m, weight 40 kN) are arranged as shown in Figure 8. Find the reactions at all contact points. All contacts are smooth. 

Answer 1

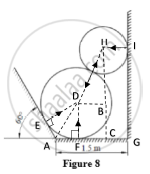
In ΔDAE and ΔDAF,
DA = DA;
∠DEA = ∠DFE;
By RHS rule , ΔDAE is congruent to ΔDAF
∠DAE = ∠DAF
∠DAE + ∠DAF = 2∠DAE = 180 – 60
∠DAE = ∠DAF = 60⁰
In ΔDAF,

`tan (60) (DF)/(AF)`

`AF = (0.75)/(tan(60) )= 0.433 m`

AG = AF + FC + CG
1.5 = 0.433 + DB + HI
1.5 – 0.433 – HI = DB
1.5 – 0.433 – 0.5 = DB
DB = 0.567 m
In ΔDBH,

Cos(D) =`(DB)/(DH) = (0.567)/(0.75+.5) = 0.4536`

`D = cos^(-1) 0.4536 = 63.025^0`
Considering cylinder A,

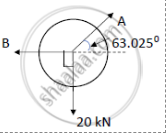
Using Lami’s theorem,

`20/sin (180-63.025) = A/(sin(90)) = B/(sin(90+63.025))`

A = 22.44 kN
B = 10.1795 kN

Considering cylinder B,

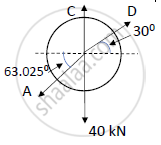
ΣFx = 0
300 Dcos(30) – A cos(63.025) = 0 …..(1)

D = 11.75 kN

ΣFy = 0

C – 40 + Dsin(30) – Asin(63.025) = 0

C =25.876 kN

The magnitudes of the reaction forces are
A = 22.44 kN
B = 10.1795 kN
C = 25.876 kN
D = 11.75 kN