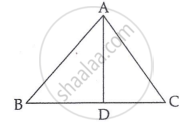
Question

D is a point on the side BC of `triangle`ABC such that `angle`ADC = `angle`BAC. Show that AC² = BC × DC.

Answer 1

Given that,

`angle`ADC = `angle`BAC

In `triangle`ADC and `triangle`BAC, we have

`angle`ADC = `angle`BAC      ...(Given)

`angle`C = `angle`C      ...(Common)

By the AA similarity criterion

`triangle`ADC ∼ `triangle`BAC

So, `(AC)/(BC) = (DC)/(AC)`

∴ AC² = BC × DC