English Medium
Academic Year: 2023-2024
Date & Time: 11th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions carefully and follow them:
- This question paper contains 38 questions. All questions are compulsory.
- Question paper is divided into FIVE sections − SECTION A, B, C, D and E.
- In section A, question number 1 to 18 are multiple choice questions (MCQs) and question number 19 and 20 are Assertion − Reason based questions of 1 mark each.
- In section B, question number 21 to 25 are very short answer (VSA) type questions of 2 marks each.
- In section C, question number 26 to 31 are short answer (SA) type questions carrying 3 marks each.
- In section D, question number 32 to 35 are long answer (LA) type questions carrying 5 marks each.
- In section E, question number 36 to 38 are case-based integrated units of assessment questions carrying 4 marks each. Internal choice is provided in 2 marks question in each case study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
- Draw neat figures wherever required. Take
- Use of calculators is NOT allowed.
For what value of k, the product of zeroes of the polynomial kx2 − 4x − 7 is 2?
Chapter:
In an A.P., if a = 8 and a10 = −19, then value of d is ______.
3
−3
Chapter:
The mid-point of the line segment joining the points (−1, 3) and
Chapter:
The curved surface area of a right circular cone of radius 7 cm is 550 sq cm. The slant height of the cone is ______.
24 cm
25 cm
22 cm
20 cm
Chapter:
If the roots of quadratic equation 4x2 − 5x + k = 0 are real and equal, then value of k is ______.
Chapter:
If probability of winning a game is p, then probability of losing the game is ______.
1 + p
−p
p − 1
1 − p
Chapter:
The distance between the points (2, −3) and (−2, 3) is ______.
5 units
10 units
Chapter:
If HCF (96, 404) = 4, then LCM (96, 404) is ______.
9600
96 × 404
404
9696
Chapter:
A card is drawn from a well shuffled deck of 52 playing cards. The probability that drawn card is a red queen, is______.
Chapter:
If a certain variable x divides a statistical data arranged in order into two equal parts, then the value of x is called the ______.
mean of the data
median
mode
range
Chapter:
The radius of a sphere is
154 cu cm
Chapter:
Which of the following cannot be the probability of an event?
52%
0.99
Chapter:
The height and radius of a right circular cone are 24 cm and 7 cm respectively. The slant height of the cone is ______.
24 cm
31 cm
26 cm
25 cm
Chapter:
Advertisements
Two dice are rolled together. The probability of getting at least one 6, is ______.
Chapter:
The diameter of a circle is of length 6 cm. If one end of the diameter is (−4, 0), the other end on x-axis is at ______.
(0, 2)
(6, 0)
(2, 0)
(4, 0)
Chapter:
The value of k for which the pair of linear equations 5x + 2y − 7 = 0 and 2x + ky + 1 = 0 don't have a solution is ______.
5
Chapter:
Two dice are rolled together. The probability of getting a double is ______.
Chapter:

Assertion (A): If PA and PB are tangents drawn to a circle with centre O from an external point P, then the quadrilateral OAPB is a cyclic quadrilateral.
Reason (R): In a cyclic quadrilateral, opposite angles are equal.
Both, Assertion (A) and Reason (R) are true. Reason (R) explains Assertion (A) completely.
Both, Assertion (A) and Reason (R) are true. Reason (R) does not explain Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
Assertion (A): Zeroes of a polynomial p(x) = x2 − 2x − 3 are −1 and 3.
Reason (R): The graph of polynomial p(x) = x2 − 2x − 3 intersects x-axis at (−1, 0) and (3, 0).
Both, Assertion (A) and Reason (R) are true. Reason (R) explains Assertion (A) completely.
Both, Assertion (A) and Reason (R) are true. Reason (R) does not explain Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
D is a point on the side BC of
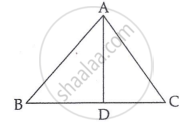
Chapter:
Solve the following pair of linear equations for x and y algebraically:
x + 2y = 9 and y − 2x = 2
Chapter:
Check whether the point (−4, 3) lies on both the lines represented by the linear equations x + y + 1 = 0 and x − y = 1.
Chapter:
Prove that
Chapter:
Show that 11 × 19 × 23 + 3 × 11 is not a prime number.
Chapter:
If sin A =
Chapter:
Advertisements
In the given figure, in ΔABC, BD and CE are perpendiculars to AC and AB respectively. Prove that: AE × BD = AD × CE.
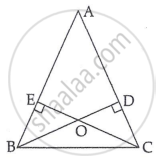
Chapter:
Two alarm clocks ring their alarms at regular intervals of 20 minutes and 25 minutes respectively. If they first beep together at 12 noon, at what time will they beep again together next time?
Chapter:
The greater of two supplementary angles exceeds the smaller by 18°. Find measures of these two angles.
Chapter:
Find the co-ordinates of the points of trisection of the line segment joining the points (−2, 2) and (7, −4).
Chapter:
Prove that:
sin6 θ + cos6 θ + 3 sin2 θ cos2 θ = 1
Chapter:
A solid is in the form of a cylinder with hemispherical ends of same radii. The total height of the solid is 20 cm and the diameter of the cylinder is 14 cm. Find the surface area of the solid.
Chapter:
A juice glass is cylindrical in shape with hemispherical raised up portion at the bottom. The inner diameter of glass is 10 cm and its height is 14 cm. Find the capacity of the glass. (use π = 3.14)
Chapter:
If A(2, −1), B(a, 4), C(−2, b) and D(−3, −2) are vertices of a parallelogram ABCD taken in order, then find the values of a and b. Also, find the length of the sides of the parallelogram.
Chapter:
In the given figure, two concentric circles with centre O have radii 14 cm and 7 cm. If ∠AOB = 30°, find the area of the shaded region.
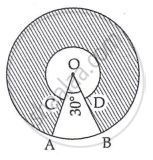
Chapter:
How many terms of the A.P. 27, 24, 21, ..... must be taken so that their sum is 105? Which term of the A.P. is zero?
Chapter:
In an A.P. of 50 terms, the sum of first 10 terms is 250 and the sum of its last 15 terms is 2625. Find the A.P. so formed.
Chapter:
A chord of a circle of radius 14 cm subtends an angle of 90° at the centre. Find the area of the corresponding minor and major segments of the circle.
Chapter:
To keep the lawn green and cool, Sadhna uses water sprinklers which rotate in circular shape and cover a particular area.
The diagram below shows the circular areas covered by two sprinklers:
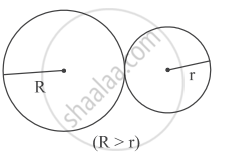

Two circles touch externally. The sum of their areas is 130π sq m and the distance between their centres is 14 m.
Based on the above information, answer the following questions:
- Obtain a quadratic equation involving R and r from above. 1
- Write a quadratic equation involving only r. 1
-
- Find the radius r and the corresponding area irrigated. 2
OR - Find the radius R and the corresponding area irrigated. 2
- Find the radius r and the corresponding area irrigated. 2
Chapter:
Gurpreet is very fond of doing research on plants. She collected some leaves from different plants and measured their lengths in mm.

The data obtained is represented in the following table:
|
Length (in mm): |
70 - 80 | 80 - 90 | 90 - 100 | 100 - 110 | 110 - 120 | 120 - 130 | 130 - 140 |
|
Number of leaves: |
3 | 5 | 9 | 12 | 5 | 4 | 2 |
Based on the above information, answer the following questions:
- Write the median class of the data. 1
- How many leaves are of length equal to or more than 10 cm? 1
-
- Find median of the data. 2
OR - Write the modal class and find the mode of the data. 2
- Find median of the data. 2
Chapter:
The picture given below shows a circular mirror hanging on the wall with a cord. The diagram represents the mirror as a circle with centre O. AP and AQ are tangents to the circle at P and Q, respectively such that AP = 30 cm and ∠PAQ = 60°.
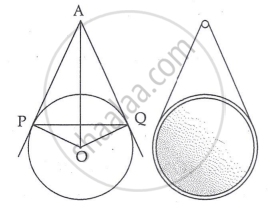
Based on the above information, answer the questions:
- Find the length PQ. 1
- Find m ∠POQ. 1
- Find the length OA. 2
OR - Find the radius of the mirror. 2
- Find the length OA. 2
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 10 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
