Question

The picture given below shows a circular mirror hanging on the wall with a cord. The diagram represents the mirror as a circle with centre O. AP and AQ are tangents to the circle at P and Q, respectively such that AP = 30 cm and ∠PAQ = 60°.

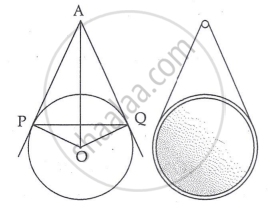
Based on the above information, answer the questions:

1. Find the length PQ.    1
2. Find m ∠POQ.    1
   1. Find the length OA.    2
      OR
   2. Find the radius of the mirror.    2

Answer 1

Given that,

AP = 30 cm

`angle`PAQ = 60°

We have,

AP = AQ = 30 cm     ...[length of tangents are equal]  

Also,

`angle`PAO = `1/2 xx ∠PAQ`

= `1/2 xx 60^circ`

= 30°

In `triangle`APM,

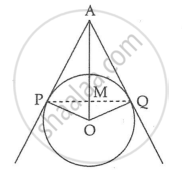
Sin 30° = `(PM)/(AP)`

`1/2 = (PM)/30`

⇒ PM = 15 cm

Also, PM = MQ = 15 cm     ...[Chord is bisected by perpendicular from centre]

PQ = 2 PM = 30 cm

(i)

Length of PQ = 30 cm

(ii)

As APOQ is a cyclic quadrilateral,

So, `angle`PAQ + `angle`POQ = 180° 

⇒ 60° + `angle`POQ = 180° 

⇒ `angle`POQ = 180° − 60° 

⇒ `angle`POQ = 120°

(iii) (a)

In `triangle`AOP,

⇒ cos 30° = `(AP)/(OA)`

⇒ `sqrt3/2 = 30/(OA)`

⇒ OA = `60/sqrt3`

⇒ OA = `20sqrt3` cm

OR (b)

In `triangle`AOP,

⇒ tan 30° = `(OP)/(AP)`

⇒ `1/sqrt3 = (OP)/30`

⇒ OP = `30/sqrt3` cm

⇒ OP = `10sqrt3` cm

Radius of mirror = `10sqrt3` cm