Advertisements
Advertisements
Question
To keep the lawn green and cool, Sadhna uses water sprinklers which rotate in circular shape and cover a particular area.
The diagram below shows the circular areas covered by two sprinklers:
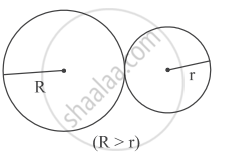

Two circles touch externally. The sum of their areas is 130π sq m and the distance between their centres is 14 m.
Based on the above information, answer the following questions:
- Obtain a quadratic equation involving R and r from above. 1
- Write a quadratic equation involving only r. 1
-
- Find the radius r and the corresponding area irrigated. 2
OR - Find the radius R and the corresponding area irrigated. 2
- Find the radius r and the corresponding area irrigated. 2
Solution
(i)
We have,
R + r = 14 ...[Given]
Also,
Sum of areas = 130π m2
⇒ πR2 + πr2 = 130π
⇒ R2 + r2 = 130 ...(i)
is the required quadratic equation.
(ii)
We have,
R + r = 14
R = 14 − r
Putting in eqn (i),
⇒ (14 − r)2 + r2 = 130
⇒ 196 + r2 − 28r + r2 = 130
⇒ 2r2 − 28r + 66 = 0
⇒ r2 − 14r + 33 = 0
Is the required quadratic equation in r only.
(iii) (a)
We have,
⇒ r2 − 14r + 33 = 0
⇒ r2 − 11r − 3r + 33 = 0
⇒ r(r − 11) − 3(r − 11) = 0
⇒ (r − 11)(r − 3) = 0
⇒ r = 11 (rejected) ...[As R > r]
So, r = 3 m
Corresponding Area irrigated = πr2 = 9π m2.
OR (b)
We have,
⇒ r2 − 14 r + 33 = 0
⇒ r2 − 11r − 3r + 33 = 0
⇒ r(r − 11) − 3(r − 11) = 0
⇒ (r − 11)(r − 3) = 0
⇒ r = 11 (rejected) ...[As R > r]
So, r = 3 m
Now,
R + r = 14
⇒ R + 3 = 14
⇒ R = 11 m
Corresponding area irrigated = πR2 = 121π m2.
