Advertisements
Advertisements
Question
Deduce the expression for the torque acting on a dipole of dipole moment `vecp` in the presence of a uniform electric field `vecE`
Solution
Dipole in a Uniform External Field
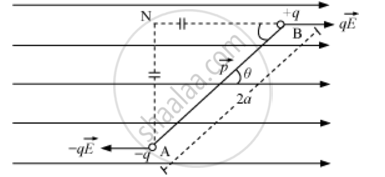
Consider an electric dipole consisting of charges −q and +q and of length 2a placed in a uniform electric field `vecE`making an angle θ with electric field.
Force on charge `-q" at "A=-qvecE("opposite to" vecE)`
Force on charge `+q" at "B=qvecE("along"vecE)`
Electric dipole is under the action of two equal and unlike parallel forces, which give rise to a torque on the dipole.
τ = Force × Perpendicular distance between the two forces
τ = qE (AN) = qE (2a sin θ)
τ = q(2a) E sinθ
τ = pE sinθ
`:.vect=vecpxxvecE`
APPEARS IN
RELATED QUESTIONS
An electric dipole with dipole moment 4 × 10−9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 104 N C−1. Calculate the magnitude of the torque acting on the dipole.
An electric dipole is placed in a uniform electric field. The net electric force on the dipole
A long bar magnet has a pole strength of 10 Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5 cm from the north pole of the magnet.
Maximum torque acting on an electric dipole of moment 3×10-29 Cm in a uniform electric field E is 6 × 10-25 Nm. Find E.
An electric dipole of dipole moment `vecP` is placed in a uniform electric field `vecE` with its axis inclined to the field. Write an expression for the torque `vecT` experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is:
- maximum
- Zero
Deduce the expression for the torque `vec"τ"` acting on a planar loop of area `vec"A"` acting on a planar loop of area `vec"B"`. If the loop is free to rotate, what would be its orientation in stable equilibrium?
Answer the following question.
Derive the expression for the torque acting on an electric dipole, when it is held in a uniform electric field. identify the orientation of the dipole in the electric field, in which it attains a stable equilibrium.
A short bar magnet of magnetic moment m = 0.32 J T–1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its
- stable, and
- unstable equilibrium?
What is the potential energy of the magnet in each case?
If the solenoid is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 × 10−2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s−1. What is the moment of inertia of the coil about its axis of rotation?
Assertion: The poles of magnet can not be separated by breaking into two pieces.
Reason: The magnetic moment will be reduced to half when a magnet is broken into two equal pieces.
Let the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator is ______.
An electric dipole of dipole moment 2 × 10-8 C-m in a uniform electric field experiences a maximum torque of 6 × 10-4 N-m. The magnitude of the electric field is ______.
