Advertisements
Advertisements
Question
Derive an expression for axial magnetic field produced by current in a circular loop.
Solution
- Consider loop of radius R carrying current I placed in x - y plane with its centre at origin O as shown in the figure below.

The magnetic field on the axis of a circular current loop of radius R - Let point P can be on z-axis at distance `vec"r"` from line element `vec"d"l` of the loop.
- Using Biot-Savart law, the magnitude of the magnetic field dB is given by dB = `mu_0/(4pi) "I" (|"d"vecl xx vec"r"|)/"r"^3`
- Any element `vec"d"l` will always be perpendicular to the vector `vec"r"` from the element to the point P. The element `vec"d"l` is in the x-y plane, while the vector `vec"r"` is in the y-z plane. Hence
`vec"d"l` × `vec"r"` = dlr
∴ dB = `mu_0/(4pi) "I" "dl"/"r"^2`
but r2 = R2 + z2
∴ dB = `mu_0/(4pi) "I" "dl"/(("z"^2 + "R"^2))` - Now, the direction of `"d"vec"B"` is perpendicular to the plane formed by `"d"vec"l"` and `vec"r"`. Its z component is dBz and the component perpendicular to the z-axis is dB⊥. The components dB⊥ when summed over, yield zero as they cancel out due to symmetry. Hence, only the z component remains.
- The net contribution along the z-axis is obtained by integrating dBz = dB cos θ over the entire loop. From figure,
cosθ = `"R"/"r" = "R"/sqrt("z"^2 + "R"^2)`
∴ Bz = `int "dB"_"z" = mu_0/(4pi) "I" int "dl"/(("z"^2 + "R"^2))cos theta`
= `mu_0/(4pi) "I" int "Rdl"/(("z"^2 + "R"^2)^{3/2})`
= `mu_0/(4pi) xx "lR"/(("z"^2 + "R"^2)^{3/2}) xx 2pi"R"`
Bz = `mu_0/2 xx "IR"^2/(("z"^2 + "R"^2)^{3/2})`
This is the magnitude of the magnetic field due to current I in the loop of radius R, on a point at P on the z-axis of the loop.
RELATED QUESTIONS
A circular loop of radius 0.0157 m carries a current 2 A. The magnetic field at the centre of the loop is ______
Calculate the value of the magnetic field at a distance of 2 cm from a very long straight wire carrying a current 5 A?
A circular coil has 150 turns and a mean diameter of 20 cm. It carries a current of 10 A. What is the strength of the magnetic field at a point on its axis at a distance of 5 m from the centre of the coil?
Two circular loop A and B of radii Rand NR respectively are made from a uniform wire. Moment of inertia of B about its axis is 3 times that of A about its axis. The value of N is ______.
A circular coil carrying current 'I' has radius 'R' and magnetic field at the centre is 'B'. At what distance from the centre along the axis of the same coil, the magnetic field will be `"B"/64`?
Magnetic induction produced at the centre of a circular loop carrying current is 'B'. The magnetic moment of the loop of radius 'R' is (µ0 = permeability of free space) ____________.
The magnetic moment of a circular coil carrying current (I), having radius (r) and number of turns (n) is proportional to ____________.
Three circular concentric wires of radii a, 2a, and 3a are carrying currents 3I, 2I, and I respectively in the anticlockwise direction. The effective magnetic field at the common center is ____________.
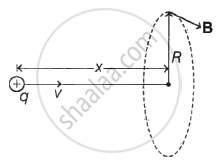
A charge q (> 0) moves towards the centre of a circular loop of radius R along its axis. The magnitude of B along the periphery of the loop is ______.
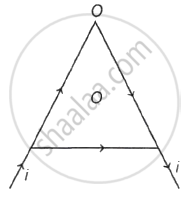
An equilateral triangle of side l is formed from a piece of wire of uniform resistance. The current i is fed as shown in the figure. The magnitude of the magnetic field at its centre O is ______.
A flat circular coil of 70 turns has a diameter of 20 cm and carries a current of 5 A. Find the magnitude of the magnetic induction at a point on the axis 20 cm from the centre of the coil.
