Question

Derive Bragg's condition for X-ray diffraction. Monochromatic X rays are
incident on a crystal. If the first order rejection is observed at an angle of 3.4•, at
what angle would second order reflection expected.

Answer 1

W.L.Bragg's explained the phenomenon of X-ray diffractionn from a single crystal shown as
follows

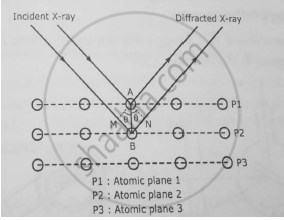
When a beam of X-rays is incident on a crystal it is scattered by individual atoms of the rich
atomic planes. Thus,each atom become a source of scattered radiation. The atomic planes
responsible for the X-ray diffraction are called BRAGG'S PLANES. Therefore, the sets of
Braggs planes constitute the crystal grating. Bragg's scattering or Bragg's diffraction is also
referred as Braggs reflection. Bragg derived a law called Bragg's law to explain the X-ray
diffraction effect. Here a beam of X-ray is incident on a set of parallel planes of a crystal. The
rays makes glancing angle e and are practically reflected from different successive
planes. The phase relationship of the scattered rays can be determined from their path
differences. Here two parallel X-rays are reflected from two consecutive planes Pr and P. The
path differences between them as shown

6=MB+BN=2MB=2ABsin8.

Here AB = d,the interplanar spacing of the crystal

 Hence                  6=2dsine

The two diffracted rays reinforce each other when they interfere constructively when their
path
difference 6 is equal to n.A
Hence,                    2dsin8=n.A is called as Bragg's Law

Numericsl solution:

Date : ` theta_1  = 3.4°`

Fonnula: 2dsine = n.λ

Solution: From equation, sineΘ ∝ n

Hence,

`sintheta_1 / (sin theta_2) = n_1 /n_2`
sin(3.4) / `sintheta_2 = 1/2`
`sintheta_2 = 0.1186`

`theta_2 = 6.8113°`

Answer.· Hence, second order reflection is expected at 6. 8113°.