Advertisements
Advertisements
Question
Derive the energy expression for an eletron is the hydrogen atom using Bohr atom model.
Solution
Bohr postulates is finds the allowed energies of the atom for different allowed orbits of the electron.
- The electron in an atom moves around the nucleus in circular orbits under the influence of Coulomb electrostatic force of attraction.
- Electrons in an atom revolve around the nucleus only in certain discrete orbits called stationary orbits where it does not radiate electromagnetic energy.
Angular momentum quantization condition,
L = `"nh" = "nh"/(2pi)`
h – planck’s constant
n – principal quantum number of the orbit. - An electron can jump from one orbit to another orbit by absorbing or emitting a photon whose energy is equal to the difference in energy (∆E) between the two orbital levels.
energy quantization condition
`delta "E" = "E"_"final" - "E"_"initial" = "hv" = "hc"/lambda`
λ – wavelength of the radiation
c – speed of light
υ – frequency of the radiationRadius of the orbit of the electron:
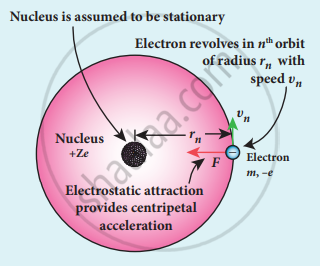
Electron revolving around the nucleus
- The nucleus has a positive charge +Ze.
- Let z be the atomic number of the atom.
- Let -e be the charge of the electron.
- The nucleus at rest and an electron revolving around the nucleus in a circular orbit of radius rn with a constant speed υn
Coulomb’s law, the force of attraction between the nucleus and the electron is
`vec"F"_"coulomb" = 1/(4 piepsilon_0) ((+ "Ze")(-"e"))/"r"_"n"^2 hat"r"`
`= - 1/(4 piepsilon_0) ("Ze"^2)/("r"_"n"^2) hat"r"` - This force provides necessary centripetal force.
`vec"F" _"centripetal" = ("mv"_"n"^2)/"r"_"n" hat"r"`
where m be the mass of the electron that moves with a velocity υn in a circular orbit.
Therfore,
`1/(4 piepsilon_0) ("Ze"^2)/("r"_"n"^2) = ("mv"_"n"^2)/"r"_"n"`
`"r"_"n" = (4piepsilon_0 ("mv"_"n""r"_"n")^2)/("Zme"^2)` ....(1)
From Bohr's assumption, the angular momentum quantization condition,
`"mv"_"n""r"_"n" = "l"_"n" = nh`,
`therefore "r"_"n" (4piepsilon_0("nh")^2)/("Zme"^2) = (4piepsilon_0"n" "h"^2)/("Zme"^2)`
`"r"_"n" = ((epsilon_0"h"^2)/(pi"me"^2))"n"^2/"Z" (therefore "h" = "h"/(2pi))`
Where n∈N ε0, n, e and π → are constant
radius of the orbit,
rn = a0 `"n"^2/"Z"`
Bohr radius a0 = `(epsilon_0"h"^2)/(pi"me"^2)`
a0 = 0.529 Å
Bohr radius is also used as unit of length called Bohr1 Bohr = 0.53 Å
For hydrogen atom Z = 1
The energy of an electron in the nth orbit:
rn = a0 n2
rn α n2
For the first orbit (ground sate)
r1 = a0
r2 = 4a0 = 4r1
r3 = 9a0 = 9r1
r4 = 16a0 = 16r1
Since the electrostatic force is a conservative force, the potential energy for the nth orbit is
`"U"_"n" = 1/(4piepsilon_0) ((+ "Ze")(- "e"))/"r"_"n" = - 1/(4piepsilon_0) "Ze"^2/"r"_"n"`
`= - 1/(4epsilon_0^2) ("Z"^2"me"^4)/("h"^2"n"^2) (therefore "r"_"n" = (epsilon_0"h"^2)/(pi"me"^2) "n"^2/"Z")`
The kinetic energy for the nth orbit
`"KE"_"n" = 1/2 "mv"_"n"^2 = "me"^4/(8epsilon_0^2 "h"^2) "Z"^2/"n"^2`
This implies that `"U"_"n" = - 2 "KE"_"n".`
Total energy in the nth orbit
`"E"_"n" = "KE"_"n" + "U"_"n" = "KE"_"n" - 2 "KE"_"n" = - "KE"_"n"`
`"E"_"n" = (- "me"^4)/(8epsilon_0^2"h"^2) "Z"^2/"n"^2`
For hydrogen atom (Z = 1),
`"E"_"n" = (- "me"^4)/(8epsilon_0^2"h"^2) 1/"n"^2`joule
`"E"_"n" = - 13.6 1/"n"^2 "eV"` -
The negative sign in the equation indicates that the electron is bound to the nucleus
-
Where n stands for a principal quantum number.
-
The energies of the excited states come closer and closer together when the principal quantum number n takes higher values.
-
The ground state energy of hydrogen (-13.6 eV) is used as a unit of energy called Rydberg (lRydberg = -13.6eV).
-
For the first orbit (ground state), the total energy of the electron is E1 = -13.6 eV.
-
For the second orbit (first excited state), the total energy of the electron is E2 = – 3.4eV.
-
For the third orbit (second excited state), the total energy of electron ie E3 = -1.51 eV and so on.
-
When the electron is taken away to an infinite distance (very far distance) from nucleus, both the potential energy and kinetic energy terms vanish and hence the total energy also vanishes.
APPEARS IN
RELATED QUESTIONS
According to the Bohr Theory, which of the following transitions in the hydrogen atom will give rise to the least energetic photon?
In J.J. Thomson e/m experiment, a beam of electron is replaced by that of muons (particle with same charge as that of electrons but mass 208 times that of electrons). No deflection condition is achieved only if
The electric potential between a proton and an electron is given by V = V0 In `("r"/"r"_0)`, where r0 is a constant. Assume that Bohr atom model is applicable to potential, then a variation of radius of nth orbit rn with the principal quantum number n is
Write down the postulates of Bohr atom model.
What is meant by excitation energy?
Write down the draw backs of the Bohr atom model.
What is distance of closest approach?
Explain the J. J. Thomson experiment to determine the specific charge of an electron.
Discuss the spectral series of hydrogen atom.
In the Bohr atom model, the frequency of transitions is given by the following expression
v = `"Rc" (1/"n"^2 - 1/"m"^2)`, where n < m
Consider the following transitions:
| Transitions | m → n |
| 1 | 3 → 2 |
| 2 | 2 → 1 |
| 3 | 3 → 1 |
Show that the frequency of these transitions obey sum rule (which is known as Ritz combination principle).
