Advertisements
Advertisements
Question
Derive the expression for resultant capacitance, when the capacitor is connected in series.
Solution
Consider three capacitors of capacitance C1, C2 and C3 connected in series with a battery of voltage V as shown in figure (a).
As soon as the battery is connected to the capacitors in series, the electrons of charge -Q are transferred from negative terminal to the right plate of C3which pushes the electrons of same amount -Q from left plate of C3 to the right plate of C2 due to electrostatic induction. Similarly, the left plate of C2 pushes the charges of Q to the right plate of which induces the positive charge +Q on the left plate of C1 At the same time, electrons of charge -Q are transferred from left plate of C1 to positive terminal of the battery.
(a)
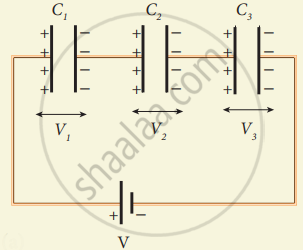
Capacitors connected in series
(b)
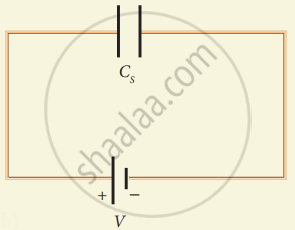
Equivalent capacitors CS
By these processes, each capacitor stores the same amount of charge Q. The capacitances of the capacitors are in general different, so that the voltage across each capacitor is also different and are denoted as V1, V2 and V3 respectively.
The total voltage across each capacitor must be equal to the voltage of the battery.
V = V1 + V2 + V3 ….. (1)
Since Q = CV, we have V = `"Q"/"C"_1 + "Q"/"C"_2 + "Q"/"C"_3`
Q = `(1/"C"_1 + 1/"C"_2 + 1/"C"_3)` .....(2)
If three capacitors in series are considered to form an equivalent single capacitor Cs shown in figure (b), then we have V = `"Q"/"C"_"s"`
Substituting this expression into equation (2) we get
V = `"Q"/"C"_"s" = "Q"(1/"C"_1 + 1/"C"_2 + 1/"C"_3)`
`1/"C"_"s" = 1/"C"_1 + 1/"C"_2 + 1/"C"_3` ...(3)
Thus, the inverse of the equivalent capacitance Cs of three capacitors connected in series is equal to the sum of the inverses of each capacitance. This equivalent capacitance Cs is always less than the smallest individual capacitance in the series.
APPEARS IN
RELATED QUESTIONS
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure . Find the total charge supplied by the battery to the inner cylinders.

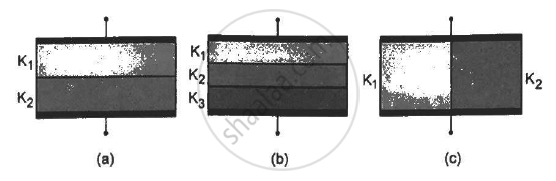
Find the capacitances of the capacitors shown in figure . The plate area is Aand the separation between the plates is d. Different dielectric slabs in a particular part of the figure are of the same thickness and the entire gap between the plates is filled with the dielectric slabs.
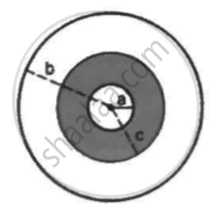
A sphercial capacitor is made of two conducting spherical shells of radii a and b. The space between the shells is filled with a dielectric of dielectric constant K up to a radius c as shown in figure . Calculate the capacitance.
An air-filled parallel-plate capacitor is to be constructed which can store 12 µC of charge when operated at 1200 V. What can be the minimum plate area of the capacitor? The dielectric strength of air is `3 xx 10^6 "Vm"^-1`
A parallel-plate capacitor with the plate area 100 cm2 and the separation between the plates 1⋅0 cm is connected across a battery of emf 24 volts. Find the force of attraction between the plates.
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system ______.
