Advertisements
Advertisements
Question
A parallel-plate capacitor with the plate area 100 cm2 and the separation between the plates 1⋅0 cm is connected across a battery of emf 24 volts. Find the force of attraction between the plates.
Solution
Area of the plates of the capacitor, A = 100 cm2 = `10^-2 "m"^2`
Separation between the plates, d = 1 cm = `10^-2 "m"`
Emf of battery, V = 24 V
Therefore,
Capacitance , `C = (∈_0A)/d = ((8.85 xx 10^-12) xx (10^-2))/(10^-2) = 8.85 xx 10^-12 V`
Energy stored in the capacitor,
`E = 1/2 CV^2 = 1/2 xx (8.85 xx 10^-12) xx (24)^2`
= `2548.8 xx 10^-12 "J"`
Force of attraction between the plates, `F = E/d = (2548.8 xx 10^-12)/(10^-2) = 2548.8 xx 10^-10 "N"`
APPEARS IN
RELATED QUESTIONS
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate The potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100 V?
The capacitance of a capacitor does not depend on
Following operations can be performed on a capacitor:
X − connect the capacitor to a battery of emf ε.
Y − disconnect the battery.
Z − reconnect the battery with polarity reversed.
W − insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
Find the charges on the three capacitors connected to a battery as shown in figure.
Take `C_1 = 2.0 uF , C_2 = 4.0 uF , C_3 = 6.0 uF and V` = 12 volts.

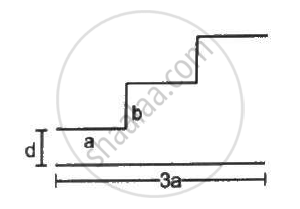
A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.
A cylindrical capacitor is constructed using two coaxial cylinders of the same length 10 cm and of radii 2 mm and 4 mm. (a) Calculate the capacitance. (b) Another capacitor of the same length is constructed with cylinders of radii 4 mm and 8 mm. Calculate the capacitance.
Convince yourself that parts (a), (b) and (c) figure are identical. Find the capacitance between the points A and B of the assembly.
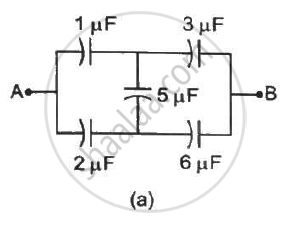
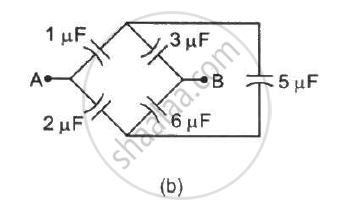
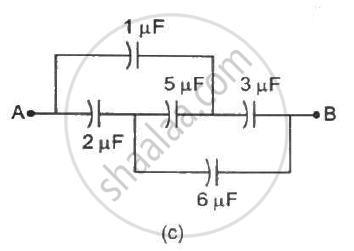
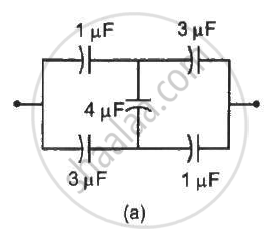
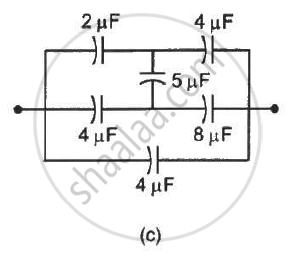
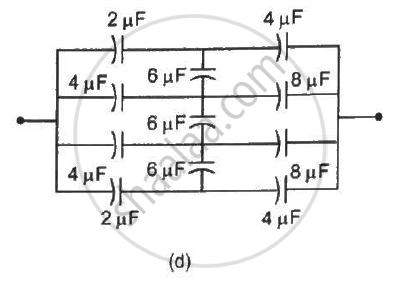
Find the equivalent capacitances of the combinations shown in figure between the indicated points.

A parallel-plate capacitor of capacitance 5 µF is connected to a battery of emf 6 V. The separation between the plates is 2 mm. (a) Find the charge on the positive plate. (b) Find the electric field between the plates. (c) A dielectric slab of thickness 1 mm and dielectric constant 5 is inserted into the gap to occupy the lower half of it. Find the capacitance of the new combination. (d) How much charge has flown through the battery after the slab is inserted?
Consider the situation shown in figure. The plates of the capacitor have plate area A and are clamped in the laboratory. The dielectric slab is released from rest with a length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period.
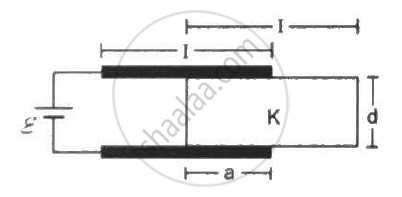
Obtain the expression for capacitance for a parallel plate capacitor.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
Can the potential function have a maximum or minimum in free space?
A capacitor of capacity 2 µF is charged to a potential difference of 12 V. It is then connected across an inductor of inductance 0.6 mH. The current in the circuit at a time when the potential difference across the capacitor is 6.0 V is ______ × 10-1A.
Read the following paragraph and answer the questions.
| A capacitor is a system of two conductors separated by an insulator. The two conductors have equal and opposite charges with a potential difference between them. The capacitance of a capacitor depends on the geometrical configuration (shape, size and separation) of the system and also on the nature of the insulator separating the two conductors. They are used to store charges. Like resistors, capacitors can be arranged in series or parallel or a combination of both to obtain the desired value of capacitance. |
- Find the equivalent capacitance between points A and B in the given diagram.

- A dielectric slab is inserted between the plates of the parallel plate capacitor. The electric field between the plates decreases. Explain.
- A capacitor A of capacitance C, having charge Q is connected across another uncharged capacitor B of capacitance 2C. Find an expression for (a) the potential difference across the combination and (b) the charge lost by capacitor A.
OR
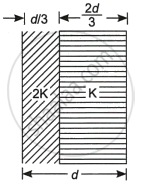
Two slabs of dielectric constants 2K and K fill the space between the plates of a parallel plate capacitor of plate area A and plate separation d as shown in the figure. Find an expression for the capacitance of the system.