Advertisements
Advertisements
Questions
Obtain the expression for capacitance for a parallel plate capacitor.
Derive an expression for the capacitance of a parallel plate capacitor with air present between the two plates.
Solution 1
Consider a capacitor with two parallel plates each of cross-sectional area A and separated by a distance d. The electric field between two infinite parallel plates is uniform and is given by E = `sigma/ε_0` where σ is the surface charge density on the plates σ = `"Q"/"A"`. If the separation distance d is very much smaller than the size of the plate (d2 << A), then the above result is used even for finite-sized
parallel plate capacitor.
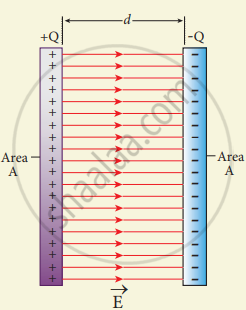
Capacitance of a parallel plate capacitor
Capacitance of a parallel plate capacitor
The electric field between the plates is
E = `"Q"/("A"ε_0)` ....(1)
Since the electric field is unifonn, the electric potential between the plates having separation d is given by
V = Ed = `"Qd"/("A"ε_0)` ....(2)
Therefore the capacitance of the capacitor is given by
C = `"Q"/"V" = "Q"/(("Qd"/("A"ε_0))) = (ε_0"A")/"d"` ....(3)
From equation (3), it is evident that capacitance is directly proportional to the area of cross-section and is inversely proportional to the distance between the plates. This can be understood from the following.
- If the area of cross-section of the capacitor plates is increased, more charges can be distributed for the same potential difference. As a result, the capacitance is increased.
- If the distance d between the two plates is reduced, the potential difference between the plates (V = Ed) decreases with E constant.
Solution 2
Derivation of the expression for the capacitance.
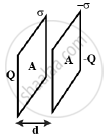
Let the two plates be kept parallel to each other separated by a distance d and the cross-sectional area of each plate is A. Electric field by a single thin plate E = `sigma/(2epsi_0)`
The total electric field between the plates E = `sigma/epsi_0` = `Q/(Aepsi_0)`
The potential difference between the plates V = Ed = `[Q/(Aε_0)]`d.
Capacitance C = `"Q"/"V" = (Aepsi_0)/d`
RELATED QUESTIONS
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
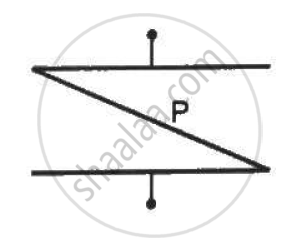
A thin metal plate P is inserted between the plates of a parallel-plate capacitor of capacitance C in such a way that its edges touch the two plates . The capacitance now becomes _________ .
The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure . Find the total charge supplied by the battery to the inner cylinders.

Convince yourself that parts (a), (b) and (c) figure are identical. Find the capacitance between the points A and B of the assembly.
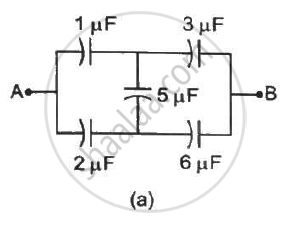
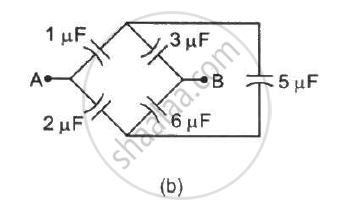
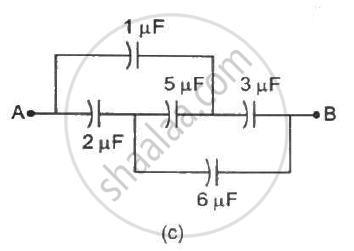
Find the capacitance of the combination shown in figure between A and B.

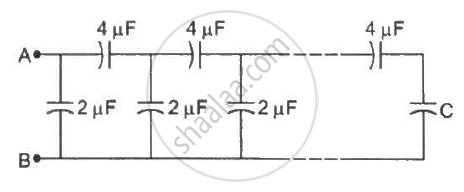
A finite ladder is constructed by connecting several sections of 2 µF, 4 µF capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance C. What value should be chosen for C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between?
The two square faces of a rectangular dielectric slab (dielectric constant 4⋅0) of dimensions 20 cm × 20 cm × 1⋅0 mm are metal-coated. Find the capacitance between the coated surfaces.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
A parallel-plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. Find the work done on the system in the process of inserting the slab.
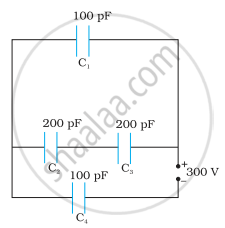
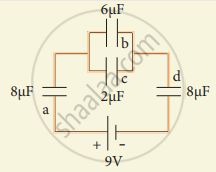
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
The work done in placing a charge of 8 × 10–18 coulomb on a condenser of capacity 100 micro-farad is ______.
Between the plates of parallel plate condenser there is 1 mm thick medium shoot of dielectric constant 4. It is charged at 100 volt. The electric field in volt/meter between the plates of capacitor is ______.
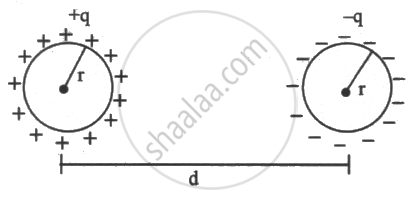
Two similar conducting spheres having charge+ q and -q are placed at 'd' seperation from each other in air. The radius of each ball is r and the separation between their centre is d (d >> r). Calculate the capacitance of the two ball system ______.
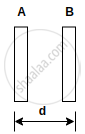
Two plates A and B of a parallel plate capacitor are arranged in such a way, that the area of each plate is S = 5 × 10-3 m 2 and distance between them is d = 8.85 mm. Plate A has a positive charge q1 = 10-10 C and Plate B has charge q2 = + 2 × 10-10 C. Then the charge induced on the plate B due to the plate A be - (....... × 10-11 )C
Obtain the equivalent capacitance of the network shown in the figure. For a 300 V supply, determine the charge on each capacitor.