Advertisements
Advertisements
Question
Find the capacitance of the combination shown in figure between A and B.

Solution
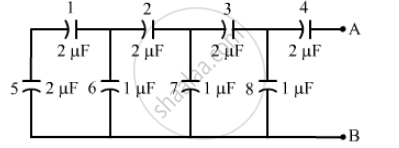
Capacitors 5 and 1 are in series.
Their equivalent capacitance, `C_(eq) = (C_1C_5)/(C_1+C_5)` =`(2 xx 2)/(2+2)` = `1 "uF"`
`therefore` `C_(eq) = 1`
Now, this capacitor system is parallel to capacitor 6. Thus, the equivalent capacitance becomes 1 + 1 = 2 μF
The above capacitor system is in series with capacitor 2. Thus, the equivalent capacitance become `(2 xx 2)/(2+2) = 1 "uF"`
The above capacitor system is in parallel with capacitor 7. Thus, the equivalent capacitance becomes 1 + 1 = 2 μF
The above capacitor system is in series with capacitor 3. Thus, the equivalent capacitance becomes `(2 xx 2)/(2+2) = 1 "uF"`
The above capacitor system is in parallel with capacitor 8. Thus, the equivalent capacitance becomes
1 + 1 = 2 μF
The above capacitor system is in series with capacitor 4. Thus, the equivalent capacitance becomes `(2 xx 2)/(2+2) = 1 "uF"`
Hence, the equivalent capacitance between points A and B of the given capacitor system is 1 μF.
APPEARS IN
RELATED QUESTIONS
Define capacitor reactance. Write its S.I units.
Two capacitors each having capacitance C and breakdown voltage V are joined in series. The capacitance and the breakdown voltage of the combination will be
When 1⋅0 × 1012 electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.
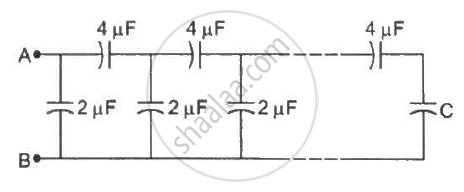
A finite ladder is constructed by connecting several sections of 2 µF, 4 µF capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance C. What value should be chosen for C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between?
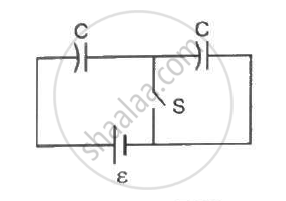
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
The two square faces of a rectangular dielectric slab (dielectric constant 4⋅0) of dimensions 20 cm × 20 cm × 1⋅0 mm are metal-coated. Find the capacitance between the coated surfaces.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
A parallel-plate capacitor has plate area 100 cm2 and plate separation 1⋅0 cm. A glass plate (dielectric constant 6⋅0) of thickness 6⋅0 mm and an ebonite plate (dielectric constant 4⋅0) are inserted one over the other to fill the space between the plates of the capacitor. Find the new capacitance.
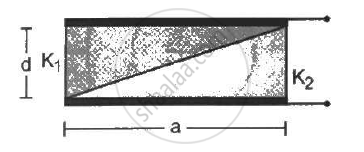
A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constant K1 and K2 are filled in the gap as shown in figure . Find the capacitance.
A sphercial capacitor is made of two conducting spherical shells of radii a and b. The space between the shells is filled with a dielectric of dielectric constant K up to a radius c as shown in figure . Calculate the capacitance.
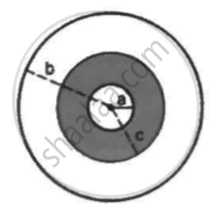
Consider an assembly of three conducting concentric spherical shell of radii a, b and c as shown in figure Find the capacitance of the assembly between the points Aand B.

Define ‘capacitance’. Give its unit.
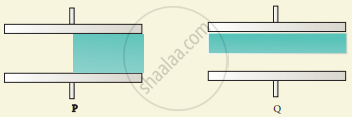
Capacitors P and Q have identical cross-sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant Er as shown in the figure. Calculate the capacitance of capacitors P and Q.
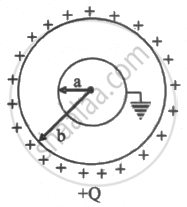
Two spherical conductors A and B of radii a and b(b > a) are placed concentrically in the air. B is given a charge +Q and A is earthed. The equivalent capacitance of the system is ______.
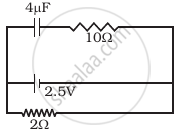
A capacitor of 4 µ F is connected as shown in the circuit (Figure). The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be ______.
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.
The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.
The new capacitance (C') in terms of the original capacitance (C0) is given by the following relation:
Two plates A and B of a parallel plate capacitor are arranged in such a way, that the area of each plate is S = 5 × 10-3 m 2 and distance between them is d = 8.85 mm. Plate A has a positive charge q1 = 10-10 C and Plate B has charge q2 = + 2 × 10-10 C. Then the charge induced on the plate B due to the plate A be - (....... × 10-11 )C