Advertisements
Advertisements
Question
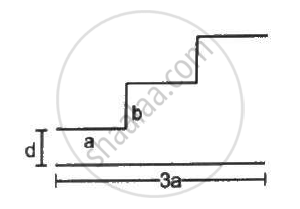
A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.
Solution
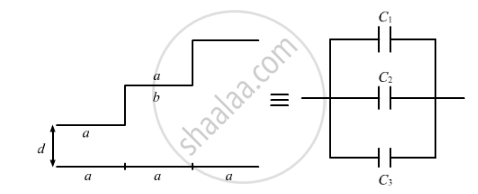
The total area of the flat plate is A. The width of each stair is the same. Therefore, the area of the surface of each stair facing the flat plate is the same, that is, `A/3` .
From the figure, it can be observed that the capacitor assembly is made up of three capacitors. The three capacitors are connected in parallel.
For capacitor C1, the area of the plates is `A/3` and the separation between the plates is d.
For capacitor C2, the area of the plates is `A/3` and the separation between the plates is (d + b).
For capacitor C3, the area of the plates is `A/3` and the separation between the plates is (d + 2b).
Therefore ,
`C_1 = (∈_0A)/(3d)`
`C_2 = (∈_0A)/(3(d+b)`
`C_3 = (∈_0A)/(3(d+2b)`
As the three capacitors are in parallel combination,
`C = C_1 + C_2 + C_3`
⇒ `C = (∈_0A)/(3d) + (∈_0A)/(3(d+b)) + (∈_0A)/(3(d+2b)`
⇒ `C = (∈_0A)/3 ((3d^2 + 6bd + 2b^2))/(d(d+b)(d+2b))`
APPEARS IN
RELATED QUESTIONS
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
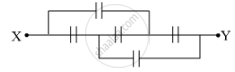
Find the equivalent capacitance of the network shown in the figure, when each capacitor is of 1 μF. When the ends X and Y are connected to a 6 V battery, find out (i) the charge and (ii) the energy stored in the network.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
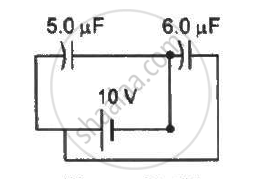
Find the charge supplied by the battery in the arrangement shown in figure.
The two square faces of a rectangular dielectric slab (dielectric constant 4⋅0) of dimensions 20 cm × 20 cm × 1⋅0 mm are metal-coated. Find the capacitance between the coated surfaces.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
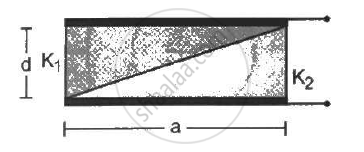
A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constant K1 and K2 are filled in the gap as shown in figure . Find the capacitance.
Obtain the expression for capacitance for a parallel plate capacitor.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
Derive the expression for resultant capacitance, when the capacitor is connected in parallel.
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system ______.
Three capacitors 2µF, 3µF, and 6µF are joined in series with each other. The equivalent capacitance is ____________.
The capacitance of a parallel plate capacitor is 60 µF. If the distance between the plates is tripled and area doubled then new capacitance will be ______.
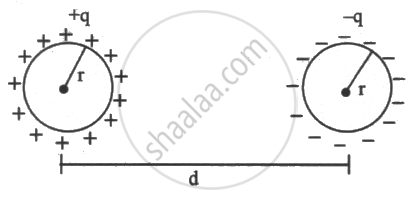
Two similar conducting spheres having charge+ q and -q are placed at 'd' seperation from each other in air. The radius of each ball is r and the separation between their centre is d (d >> r). Calculate the capacitance of the two ball system ______.
Calculate equivalent capacitance of the circuit shown in the Figure given below: