Advertisements
Advertisements
Question
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
Solution
As the capacitance of the capacitor,
`C'=(in_0KA)/(d')=(in_0KA)/(2d)=1/2C " ...1"`
Energy stored in the capacitor is
`U=Q^2/(2C)`
`U'=Q^2/(2C')=Q^2/(2(1/2)C)=2(Q^2/(2C))2U " from 1"`
Therefore, when the distance between the plates is doubled, the capacitance reduces to half. Therefore, energy stored in the capacitor becomes double.
APPEARS IN
RELATED QUESTIONS
When an AC source is connected to an ideal capacitor, show that the average power supplied by the source over a complete cycle is zero
Define capacitor reactance. Write its S.I units.
A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
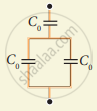
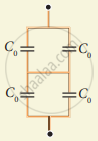
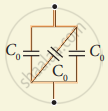
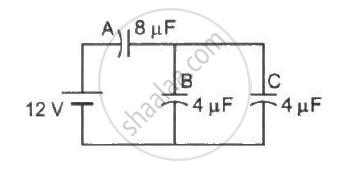
Find the charge appearing on each of the three capacitors shown in figure .
Find the capacitance of the combination shown in figure between A and B.

A parallel-plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. Find the work done on the system in the process of inserting the slab.
If the voltage applied on a capacitor is increased from V to 2V, choose the correct conclusion.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
Calculate the resultant capacitances for each of the following combinations of capacitors.
Read the following paragraph and answer the questions.
| A capacitor is a system of two conductors separated by an insulator. The two conductors have equal and opposite charges with a potential difference between them. The capacitance of a capacitor depends on the geometrical configuration (shape, size and separation) of the system and also on the nature of the insulator separating the two conductors. They are used to store charges. Like resistors, capacitors can be arranged in series or parallel or a combination of both to obtain the desired value of capacitance. |
- Find the equivalent capacitance between points A and B in the given diagram.

- A dielectric slab is inserted between the plates of the parallel plate capacitor. The electric field between the plates decreases. Explain.
- A capacitor A of capacitance C, having charge Q is connected across another uncharged capacitor B of capacitance 2C. Find an expression for (a) the potential difference across the combination and (b) the charge lost by capacitor A.
OR
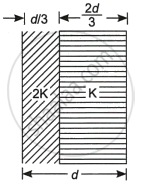
Two slabs of dielectric constants 2K and K fill the space between the plates of a parallel plate capacitor of plate area A and plate separation d as shown in the figure. Find an expression for the capacitance of the system.