Advertisements
Advertisements
प्रश्न
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
उत्तर
As the capacitance of the capacitor,
`C'=(in_0KA)/(d')=(in_0KA)/(2d)=1/2C " ...1"`
Energy stored in the capacitor is
`U=Q^2/(2C)`
`U'=Q^2/(2C')=Q^2/(2(1/2)C)=2(Q^2/(2C))2U " from 1"`
Therefore, when the distance between the plates is doubled, the capacitance reduces to half. Therefore, energy stored in the capacitor becomes double.
APPEARS IN
संबंधित प्रश्न
A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled, how will the following change?
(i) charge stored by the capacitor.
(ii) Field strength between the plates.
(iii) Energy stored by the capacitor.
Justify your answer in each case.
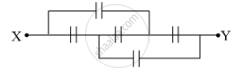
Find the equivalent capacitance of the network shown in the figure, when each capacitor is of 1 μF. When the ends X and Y are connected to a 6 V battery, find out (i) the charge and (ii) the energy stored in the network.
Two metal spheres of capacitance C1 and C2 carry some charges. They are put in contact and then separated. The final charges Q1 and Q2 on them will satisfy
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
A capacitor of capacitance 2⋅0 µF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4⋅0 µF as shown in figure . Find (a) the charge on each of the two capacitors after the connection, (b) the electrostatic energy stored in each of the two capacitors and (c) the heat produced during the charge transfer from one capacitor to the other.

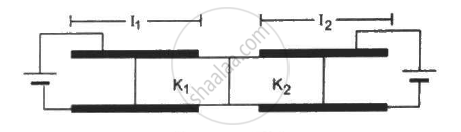
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
The variation of inductive reactance (XL) of an inductor with the frequency (f) of the ac source of 100 V and variable frequency is shown in fig.

(i) Calculate the self-inductance of the inductor.
(ii) When this inductor is used in series with a capacitor of unknown value and resistor of 10 Ω at 300 s–1, maximum power dissipation occurs in the circuit. Calculate the capacitance of the capacitor.
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
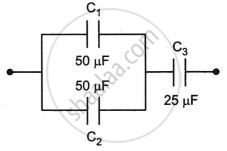
Calculate equivalent capacitance of the circuit shown in the Figure given below: