Advertisements
Advertisements
प्रश्न
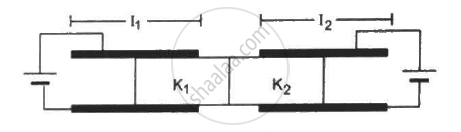
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
उत्तर
Let the potential of the battery connected to the left capacitor be V1 and that of the battery connected to the right capacitor be V2.
Considering the left capacitor,
Let the length of the part of the slab inside the capacitor be x.
The left capacitor can be considered to be two capacitors in parallel.
The capacitances of the two capacitors in parallel are :-
`C_1 = (K_1∈_0bx)/d` , `C_2 = (∈_0b(l_1 - x))/d`
C1 is the part of the capacitor having the dielectric inserted in it and C2 is the capacitance of the part of the capacitor without dielectric.
As, C1 and C2 are in parallel.
Therefore, the net capacitance is given by
`C = C_1 + C_2`
`C = (K_1∈_0bx)/d + (∈_0b(l_1 - x))/d`
`C = (∈_0b)/d [l_1 + x(K_1 - 1)]`
Therefore, the potential energy stored in the left capacitor will be
`U = 1/2CV_1^2`
`U = (∈_0bV_1^2)/(2d)[l_1 + x(K_1 - 1)] ..........(1)`
The dielectric slab is attracted by the electric field of the capacitor and applies a force in left direction.
Let us consider electric force of magnitude F pulls the slab in left direction.
Let there be an infinitesimal displacement dx in left direction by the force F.
The work done by the force = F.dx
Let us consider a small displacement dx of the slab in the inward direction. The capacitance will increase, therefore the energy of the capacitor will also increase. In order to maintain constant voltage, the battery will supply extra charges, therefore the battery will do work.
Work done by the battery = change in energy of capacitor + work done by the force F on the capacitor
`dW_B = dU + dW_F`
Let the charge dq is supplied by the battery, and the change in the capacitor be dC
`dW_B = (dq).V = (dC). V^2`
`dU = 1/2(dC).V^2`
`(dC).V^2 = 1/2(dC).V^2 + F.dx`
`1/2(dC).V^2 = F.dx`
`⇒ F = 1/2 (dC)/dxV_1^2`
`⇒ F = 1/2d/dx ((∈_0b)/d[l_1 + x(K_1 - 1)])V_1^2`
`⇒ F = (∈_0bV_1^2(K_1 - 1))/(2d)`
`⇒ V_1^2 = (F xx 2d)/(∈_0b(K_1 - 1)) ⇒ V_1 = sqrt ((F xx 2d)/(∈_0b(K_1 - 1)))`
Similarly, for the right side the voltage of the battery is given by
`V_2 = sqrt ((F xx 2d)/(∈_0b(K_2 - 1)))`
Thus , the ratio of the voltages is given by
`V_1/V_2 = sqrt ((F xx 2d)/(∈_0b(K_1 - 1)))/sqrt ((F xx 2d)/(∈_0b(K_2 - 1))`
`⇒ V_1/V_2 = (sqrt(K_2 -1))/(sqrt(K_1 - 1))`
Thus, the ratio of the emfs of the left battery to the right battery is `V_1/V_2 = (sqrt(K_2 -1))/(sqrt(K_1 - 1))`
APPEARS IN
संबंधित प्रश्न
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
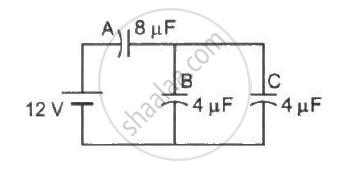
Find the charge appearing on each of the three capacitors shown in figure .
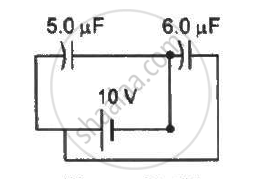
Take `C_1 = 4.0 "uF" and C_2 = 6.0 "uF"` in figure . Calculate the equivalent capacitance of the combination between the points indicated.

Find the charge supplied by the battery in the arrangement shown in figure.
Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
Each of the capacitors shown in figure has a capacitance of 2 µF. find the equivalent capacitance of the assembly between the points A and B. Suppose, a battery of emf 60 volts is connected between A and B. Find the potential difference appearing on the individual capacitors.
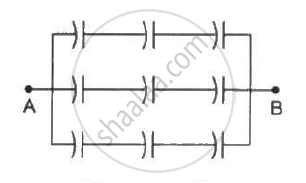
Find the capacitance of the combination shown in figure between A and B.

Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
Obtain an expression for equivalent capacitance when three capacitors C1, C2 and C3 are connected in series.
A parallel plate capacitor stores a charge Q at a voltage V. Suppose the area of the parallel plate capacitor and the distance between the plates are each doubled then which is the quantity that will change?
Obtain the expression for capacitance for a parallel plate capacitor.
Explain in detail the effect of a dielectric placed in a parallel plate capacitor.
When air is replaced by a dielectric medium of constant K, the maximum force of attraction between two charges separated by a distance ______.
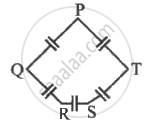
Five capacitor each of capacitance value C are connected as shown in the figure. The ratio of capacitance between P to R, and the capacitance between P and Q is ______.
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
A capacitor has charge 50 µC. When the gap between the plate is filled with glass wool, then 120 µC charge flows through the battery to capacitor. The dielectric constant of glass wool is ______.
