Advertisements
Advertisements
Question
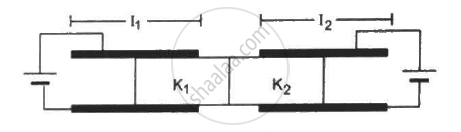
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
Solution
Let the potential of the battery connected to the left capacitor be V1 and that of the battery connected to the right capacitor be V2.
Considering the left capacitor,
Let the length of the part of the slab inside the capacitor be x.
The left capacitor can be considered to be two capacitors in parallel.
The capacitances of the two capacitors in parallel are :-
`C_1 = (K_1∈_0bx)/d` , `C_2 = (∈_0b(l_1 - x))/d`
C1 is the part of the capacitor having the dielectric inserted in it and C2 is the capacitance of the part of the capacitor without dielectric.
As, C1 and C2 are in parallel.
Therefore, the net capacitance is given by
`C = C_1 + C_2`
`C = (K_1∈_0bx)/d + (∈_0b(l_1 - x))/d`
`C = (∈_0b)/d [l_1 + x(K_1 - 1)]`
Therefore, the potential energy stored in the left capacitor will be
`U = 1/2CV_1^2`
`U = (∈_0bV_1^2)/(2d)[l_1 + x(K_1 - 1)] ..........(1)`
The dielectric slab is attracted by the electric field of the capacitor and applies a force in left direction.
Let us consider electric force of magnitude F pulls the slab in left direction.
Let there be an infinitesimal displacement dx in left direction by the force F.
The work done by the force = F.dx
Let us consider a small displacement dx of the slab in the inward direction. The capacitance will increase, therefore the energy of the capacitor will also increase. In order to maintain constant voltage, the battery will supply extra charges, therefore the battery will do work.
Work done by the battery = change in energy of capacitor + work done by the force F on the capacitor
`dW_B = dU + dW_F`
Let the charge dq is supplied by the battery, and the change in the capacitor be dC
`dW_B = (dq).V = (dC). V^2`
`dU = 1/2(dC).V^2`
`(dC).V^2 = 1/2(dC).V^2 + F.dx`
`1/2(dC).V^2 = F.dx`
`⇒ F = 1/2 (dC)/dxV_1^2`
`⇒ F = 1/2d/dx ((∈_0b)/d[l_1 + x(K_1 - 1)])V_1^2`
`⇒ F = (∈_0bV_1^2(K_1 - 1))/(2d)`
`⇒ V_1^2 = (F xx 2d)/(∈_0b(K_1 - 1)) ⇒ V_1 = sqrt ((F xx 2d)/(∈_0b(K_1 - 1)))`
Similarly, for the right side the voltage of the battery is given by
`V_2 = sqrt ((F xx 2d)/(∈_0b(K_2 - 1)))`
Thus , the ratio of the voltages is given by
`V_1/V_2 = sqrt ((F xx 2d)/(∈_0b(K_1 - 1)))/sqrt ((F xx 2d)/(∈_0b(K_2 - 1))`
`⇒ V_1/V_2 = (sqrt(K_2 -1))/(sqrt(K_1 - 1))`
Thus, the ratio of the emfs of the left battery to the right battery is `V_1/V_2 = (sqrt(K_2 -1))/(sqrt(K_1 - 1))`
APPEARS IN
RELATED QUESTIONS
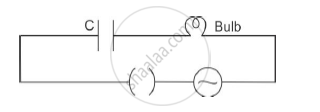
A bulb is connected in series with a variable capacitor and an AC source as shown. What happens to the brightness of the bulb when the key is plugged in and capacitance of the capacitor is gradually reduced?
A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled, how will the following change?
(i) charge stored by the capacitor.
(ii) Field strength between the plates.
(iii) Energy stored by the capacitor.
Justify your answer in each case.
Define capacitor reactance. Write its S.I units.
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
(i) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2 µF capacitance.
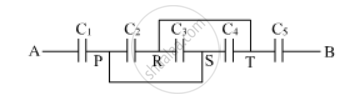
(ii) If a dc source of 7 V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network?
The equivalent capacitance of the combination shown in the figure is _________ .
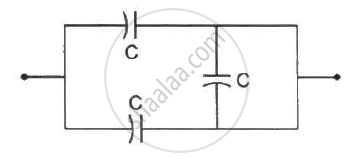
Following operations can be performed on a capacitor:
X − connect the capacitor to a battery of emf ε.
Y − disconnect the battery.
Z − reconnect the battery with polarity reversed.
W − insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
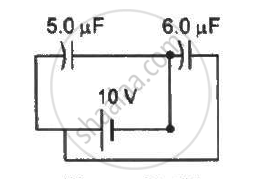
Take `C_1 = 4.0 "uF" and C_2 = 6.0 "uF"` in figure . Calculate the equivalent capacitance of the combination between the points indicated.

Find the charge supplied by the battery in the arrangement shown in figure.
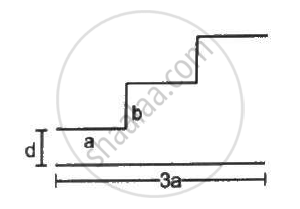
A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.
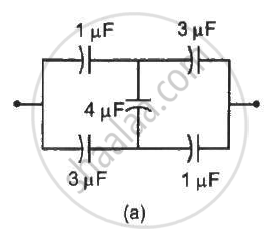
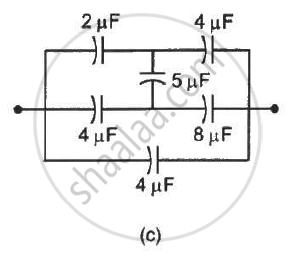
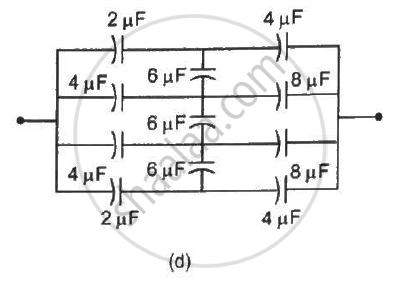
Find the equivalent capacitances of the combinations shown in figure between the indicated points.

Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
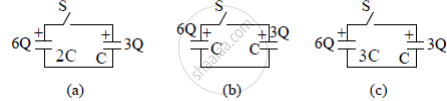
Three circuits, each consisting of a switch 'S' and two capacitors, are initially charged, as shown in the figure. After the switch has been closed, in which circuit will the charge on the left-hand capacitor
(i) increase,
(ii) decrease, and
(iii) remains the same? Give reasons.
Obtain the expression for energy stored in the parallel plate capacitor.
- Charge on each capacitor remains same and equals to the main charge supplied by the battery.
- Potential difference and energy distribute in the reverse ratio of capacitance.
- Effective capacitance is even les than the least of teh individual capacitances.
Consider two conducting spheres of radii R1 and R2 with R1 > R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
The material filled between the plates of a parallel plate capacitor has a resistivity of 200Ωm. The value of the capacitance of the capacitor is 2 pF. If a potential difference of 40V is applied across the plates of the capacitor, then the value of leakage current flowing out of the capacitor is ______.
(given the value of relative permittivity of a material is 50.)
A 5µF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 µF capacitor If the energy change during the charge redistribution is `"X"/100`J then value of X to the 100 nearest integer is ______.
Read the following paragraph and answer the questions.
| A capacitor is a system of two conductors separated by an insulator. The two conductors have equal and opposite charges with a potential difference between them. The capacitance of a capacitor depends on the geometrical configuration (shape, size and separation) of the system and also on the nature of the insulator separating the two conductors. They are used to store charges. Like resistors, capacitors can be arranged in series or parallel or a combination of both to obtain the desired value of capacitance. |
- Find the equivalent capacitance between points A and B in the given diagram.

- A dielectric slab is inserted between the plates of the parallel plate capacitor. The electric field between the plates decreases. Explain.
- A capacitor A of capacitance C, having charge Q is connected across another uncharged capacitor B of capacitance 2C. Find an expression for (a) the potential difference across the combination and (b) the charge lost by capacitor A.
OR
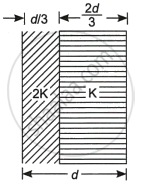
Two slabs of dielectric constants 2K and K fill the space between the plates of a parallel plate capacitor of plate area A and plate separation d as shown in the figure. Find an expression for the capacitance of the system.