Advertisements
Advertisements
Question
Read the following paragraph and answer the questions.
| A capacitor is a system of two conductors separated by an insulator. The two conductors have equal and opposite charges with a potential difference between them. The capacitance of a capacitor depends on the geometrical configuration (shape, size and separation) of the system and also on the nature of the insulator separating the two conductors. They are used to store charges. Like resistors, capacitors can be arranged in series or parallel or a combination of both to obtain the desired value of capacitance. |
- Find the equivalent capacitance between points A and B in the given diagram.

- A dielectric slab is inserted between the plates of the parallel plate capacitor. The electric field between the plates decreases. Explain.
- A capacitor A of capacitance C, having charge Q is connected across another uncharged capacitor B of capacitance 2C. Find an expression for (a) the potential difference across the combination and (b) the charge lost by capacitor A.
OR
Two slabs of dielectric constants 2K and K fill the space between the plates of a parallel plate capacitor of plate area A and plate separation d as shown in the figure. Find an expression for the capacitance of the system.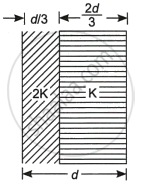
Solution
- The given circuit can be redrawn as it is a balanced Wheatstone bridge.
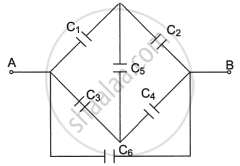
i.e., `C_1/C_2 = C_3/C_4 = C/C = 1/1`
So, Cs can be neglected.
So, the equivalent capacitance between A and B,
`C_{eq} = ((1 xx 1)/(1 + 1) + (1 xx 1)/(1 + 1) + 1)C = 2C` - Total charge of the capacitor remains conserved on the introduction of a dielectric slab. Also, the capacitance of the capacitor increases to K time of its original value.
∴ CV = C'V = KC.V (since Q = Q')
⇒ `V = V/K`
Now electric field,
`E = V/d = ((V"/"K))/d`
= `(V/d)(1/K) = E/K`
So, on introducing a dielectric medium.
The electric field reduces by `(1/K)` times its original value. - (a) The initial charge on capacitor Q = CV.
This capacitor gets connected to another parallel. So total capacitance will be
C' = C + 2C = 3C
The potential difference across this combination will be VC·
`V_C = Q/C^' = Q/(3C)`
As both the capacitors are connected in parallel, therefore, the voltage of both will be the same.
(b) Charges on both capacitors,
`Q_A = CV_C = C. Q/(3C) = Q/3`
`Q_B = 2CV_C = 2C. Q/(3C) = 2/3Q`
∴ Charge lost by capacitor A = `1/3Q`
OR
The effective capacitance in series,
C = `(Kepsi_0A)/d`
C = `(C_1C_2)/(C_1 + C_2)`
`C_1 = (2Kepsi_0A)/(d"/"3), C_2 = (Kepsi_0A)/(2d"/"3)`
C = `(C_1C_2)/(C_1 + C_2)`
= `(((2Kepsi_0A xx 3)/d) ((3Kepsi_0A)/(2d)))/((Kepsi_0A)/d(6 + 3/2))`
= `(9Kepsi_0A xx 2)/(15d)`
= `(6Kepsi_0A)/(5d)`
APPEARS IN
RELATED QUESTIONS
Three identical capacitors C1, C2 and C3 of capacitance 6 μF each are connected to a 12 V battery as shown.
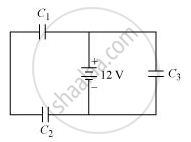
Find
(i) charge on each capacitor
(ii) equivalent capacitance of the network
(iii) energy stored in the network of capacitors
Following operations can be performed on a capacitor:
X − connect the capacitor to a battery of emf ε.
Y − disconnect the battery.
Z − reconnect the battery with polarity reversed.
W − insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
Each of the plates shown in figure has surface area `(96/∈_0) xx 10^-12` Fm on one side and the separation between the consecutive plates is 4⋅0 mm. The emf of the battery connected is 10 volts. Find the magnitude of the charge supplied by the battery to each of the plates connected to it.
A parallel-plate capacitor has plate area 100 cm2 and plate separation 1⋅0 cm. A glass plate (dielectric constant 6⋅0) of thickness 6⋅0 mm and an ebonite plate (dielectric constant 4⋅0) are inserted one over the other to fill the space between the plates of the capacitor. Find the new capacitance.
A parallel-plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. Find the work done on the system in the process of inserting the slab.
Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
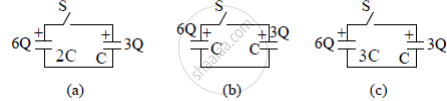
Three circuits, each consisting of a switch 'S' and two capacitors, are initially charged, as shown in the figure. After the switch has been closed, in which circuit will the charge on the left-hand capacitor
(i) increase,
(ii) decrease, and
(iii) remains the same? Give reasons.
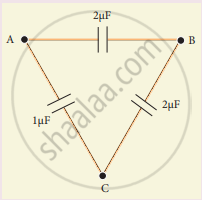
Three capacitors are connected in a triangle as shown in the figure. The equivalent capacitance between points A and C is ______.
When air is replaced by a dielectric medium of constant K, the maximum force of attraction between two charges separated by a distance ______.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of final charges on A and B.
