Advertisements
Advertisements
Question
Consider the situation shown in figure (31-E29). The width of each plate is b. The capacitor plates are rigidly clamped in the laboratory and connected to a battery of emf ε. All surfaces are frictionless. Calculate the value of M for which the dielectric slab will stay in equilibrium.

Solution
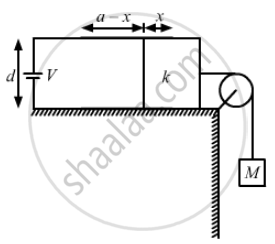
Let the potential of the battery connected to the capacitor be V.
Let the length of the part of the slab inside the capacitor be x.
The capacitor can be considered to be two capacitors in parallel.
The capacitances of the two capacitors in parallel are :-
`C_1 = (K_1∈_0bx)/d` , `C_2 = (∈_0b(l_1 - x))/d`
C1 is the part of the capacitor having the dielectric inserted in it and C2 is the capacitance of the part of the capacitor without dielectric.
As, C1 and C2 are in parallel.
Therefore, the net capacitance is given by
`C = C_1 + C_2`
`C = (K_1∈_0bx)/d + (∈_0b(l_1 - x))/d`
`C = (∈_0b)/d [l_1 + x(K_1 - 1)]`
The dielectric slab is attracted by the electric field of the capacitor and applies a force in left direction.
Let us consider electric force of magnitude F pulls the slab in left direction.
Let there be an infinitesimal displacement dx in left direction by the force F.
The work done by the force = F.dx
Let the potential of the battery connected to the left capacitor be V1 and that of the battery connected with the right capacitor be V2.
With the displacement of slab, the capacitance will increase, therefore the energy of the capacitor will also increase. In order to maintain constant voltage, the battery will supply extra charges, therefore the battery will do work.
Work done by the battery = change in energy of capacitor + work done by the force F on the capacitor
`dW_B = dU + dW_F`
Let the charge dq is supplied by the battery, and the change in the capacitor be dC
`dW_B = (dq).V = (dC).V^2`
`dU = 1/2(dC). V^2`
`(dC). V^2 = 1/2 (dC). V^2 + F.dx`
`1/2 (dC). V^2 = F.dx`
`⇒ F = 1/2 (dC)/dx V_1^2`
`⇒ F = 1/2 d/dx ((∈_0b)/d[l_1 + x(K_1 - 1)])V_1^2`
`⇒ F= (∈_0bV_1^2(K_1 - 1))/(2d)`
To keep the dielectric slab in equilibrium, the electrostatic force on it must be counteracted by the weight of the block attached.
Therefore,
`(∈_0bV^2)/(2d)(K-1) = Mg`
`⇒ M = (∈_0bV^2)/(2dg)(K-1)`
APPEARS IN
RELATED QUESTIONS
Two charges 5 × 10−8 C and −3 × 10−8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
An electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is aligned parallel to the field. Find the work done in rotating it through the angle of 180°.
Derive an expression for the electric potential at any point along the axial line of an electric dipole.
Which of the following is correct for energy of a dipole in a uniform electric field?
The electric potential at a point on the equatorial line of an electric dipole is ______.
A hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10 V. The potential at a distance of 2 cm from the centre of the sphere is ______.
An electric field of 1000 V/m is applied to an electric dipole at angle of 45°. The value of electric dipole moment is 10-29 C.m. What is the potential energy of the electric dipole?
A point P lies at a distance x from the midpoint of an electric dipole on its axis. The electric potential at point P is proportional to ______.
