Advertisements
Advertisements
Question
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
Solution
Radius of the outer shell = r1
Radius of the inner shell = r2
The inner surface of the outer shell has charge +Q.
The outer surface of the inner shell has induced charge −Q.
Potential difference between the two shells is given by,
`"V" = "Q"/(4piin_0"r"_2) - "Q"/(4piin_0"r"_1)`
Where,
`in_0` = Permittivity of free space
`"V" ="Q"/(4piin_0)[1/"r"_2 - 1/"r"_1]`
= `("Q"("r"_1 - "r"_2))/(4piin_0"r"_1"r"_2]`
Capacitance of the given system is given by
C = `"Charge (Q)"/"Potenstial difference (V)"`
= `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`
Hence, proved.
APPEARS IN
RELATED QUESTIONS
When an AC source is connected to an ideal capacitor, show that the average power supplied by the source over a complete cycle is zero
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
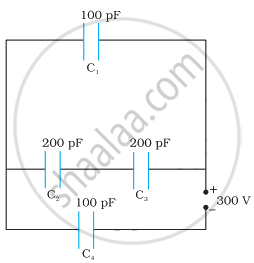
Obtain the equivalent capacitance of the network in Figure. For a 300 V supply, determine the charge and voltage across each capacitor.
As `C = (1/V) Q` , can you say that the capacitance C is proportional to the charge Q?
Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
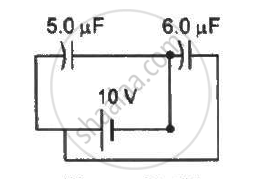
Find the charge supplied by the battery in the arrangement shown in figure.
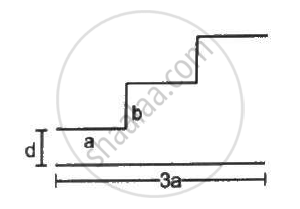
A capacitor is made of a flat plate of area A and a second plate having a stair-like structure as shown in figure . The width of each stair is a and the height is b. Find the capacitance of the assembly.
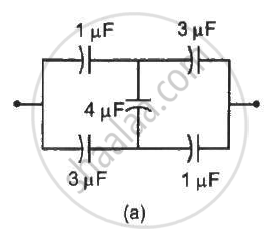
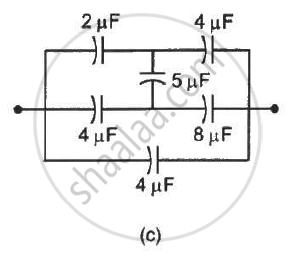
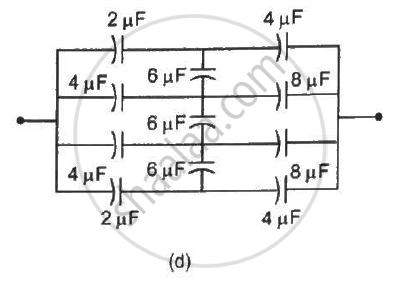
Find the equivalent capacitances of the combinations shown in figure between the indicated points.

Find the capacitance of the combination shown in figure between A and B.

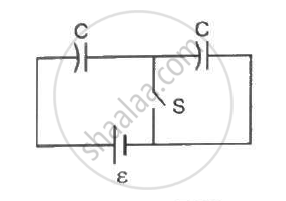
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
A 5⋅0 µF capacitor is charged to 12 V. The positive plate of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
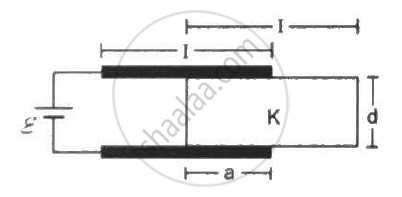
Consider the situation shown in figure. The plates of the capacitor have plate area A and are clamped in the laboratory. The dielectric slab is released from rest with a length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period.
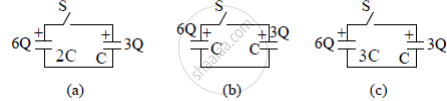
Three circuits, each consisting of a switch 'S' and two capacitors, are initially charged, as shown in the figure. After the switch has been closed, in which circuit will the charge on the left-hand capacitor
(i) increase,
(ii) decrease, and
(iii) remains the same? Give reasons.
The variation of inductive reactance (XL) of an inductor with the frequency (f) of the ac source of 100 V and variable frequency is shown in fig.

(i) Calculate the self-inductance of the inductor.
(ii) When this inductor is used in series with a capacitor of unknown value and resistor of 10 Ω at 300 s–1, maximum power dissipation occurs in the circuit. Calculate the capacitance of the capacitor.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
- Charge on each capacitor remains same and equals to the main charge supplied by the battery.
- Potential difference and energy distribute in the reverse ratio of capacitance.
- Effective capacitance is even les than the least of teh individual capacitances.
A capacitor of capacity 2 µF is charged to a potential difference of 12 V. It is then connected across an inductor of inductance 0.6 mH. The current in the circuit at a time when the potential difference across the capacitor is 6.0 V is ______ × 10-1A.
