Advertisements
Advertisements
Question
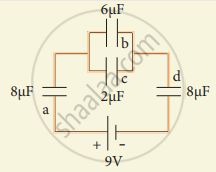
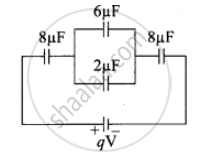
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
Advertisements
Solution
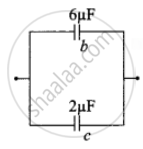
Capacitor b and c in parallel combination
Cp = Cb + Cc = (6 + 2) μF = 8 μF
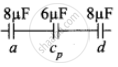
Capacitor a, cp and d are in series combination, so the resulatant copacitance
`1/"C"_"s" = 1/"C"_"a" + 1/"C"_"cp" + 1/"C"_"d"`
`= 1/8 + 1/8 + 1/8 = 3/8`
`"C"_"s" = 8/3` μF
- Charge on each capacitor,
Charge on capacitor a, Qa = Cs V = `8/3 xx 9`
Qa = 24 μC
Charge on capacitor, d, Qd = Cs V = `8/3 xx 9`
Qd = 24 μC
Capacitor b and c in parallel
Charge on capacitor, b, Qb = `6/3 xx 9` = 18
Qb = 18 μC
Charge on capacitor, c, Qc = `2/3 xx 9` = 6
Qc = 6 μC - Potential difference across each capacitor, V = `"q"/"c"`
Capacitor Ca, Va = `"q"_"a"/"C"_"a" = (24 xx 10^6)/(8 xx 10^6)` = 3 V
Capacitor Cb, Vb = `"q"_"b"/"C"_"b" = (18 xx 10^6)/(6 xx 10^6)` = 3 V
Capacitor Cc, Vc = `"q"_"c"/"C"_"c" = (6 xx 10^6)/(2 xx 10^6)` = 3 V
Capacitor Cd, Vd = `"q"_"d"/"C"_"d" = (24 xx 10^6)/(8 xx 10^6)` = 3 V - Energy stores in a capacitor, U = `1/2` CV2
Energy in capacitor Ca, Ua = `1/2 "C"_"a" "V"_"a"^2 = 1/2 xx 8 xx 10^-6 xx (3)^2`
Ua = 36 μJ
Capacitor Cb, Ub = `1/2 "C"_"b" "V"_"b"^2 = 1/2 xx 6 xx 10^-6 xx (3)^2`
Ua = 27 μJ
Cc, Uc = `1/2 "C"_"c" "V"_"c"^2 = 1/2 xx 2 xx 10^-6 xx (3)^2`
Ua = 9 μJ
Cd, Ud = `1/2 "C"_"d" "V"_"d"^2 = 1/2 xx 8 xx 10^-6 xx (3)^2`
Ua = 36 μJ
APPEARS IN
RELATED QUESTIONS
Three identical capacitors C1, C2 and C3 of capacitance 6 μF each are connected to a 12 V battery as shown.
Find
(i) charge on each capacitor
(ii) equivalent capacitance of the network
(iii) energy stored in the network of capacitors
Three capacitors of capacitances 6 µF each are available. The minimum and maximum capacitances, which may be obtained are
Each of the plates shown in figure has surface area `(96/∈_0) xx 10^-12` Fm on one side and the separation between the consecutive plates is 4⋅0 mm. The emf of the battery connected is 10 volts. Find the magnitude of the charge supplied by the battery to each of the plates connected to it.
The two square faces of a rectangular dielectric slab (dielectric constant 4⋅0) of dimensions 20 cm × 20 cm × 1⋅0 mm are metal-coated. Find the capacitance between the coated surfaces.
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system ______.
Two similar conducting spheres having charge+ q and -q are placed at 'd' seperation from each other in air. The radius of each ball is r and the separation between their centre is d (d >> r). Calculate the capacitance of the two ball system ______.
A capacitor has charge 50 µC. When the gap between the plate is filled with glass wool, then 120 µC charge flows through the battery to capacitor. The dielectric constant of glass wool is ______.
Two identical capacitors are connected as shown and have an initial charge of Q0. The separation between the plates of each capacitor is d0. Suddenly the left plate of the upper capacitor and right plate of the lower capacitor start moving with speed v towards the left while the other plate of each capacitor remains fixed. `("given" (Q_0V)/(2d_0) = 10 A)`. The value of current in the circuit is ______ A.
