Advertisements
Advertisements
प्रश्न
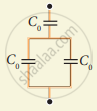
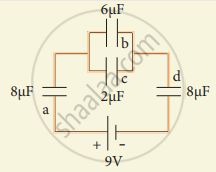
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
उत्तर
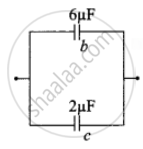
Capacitor b and c in parallel combination
Cp = Cb + Cc = (6 + 2) μF = 8 μF
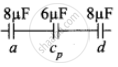
Capacitor a, cp and d are in series combination, so the resulatant copacitance
`1/"C"_"s" = 1/"C"_"a" + 1/"C"_"cp" + 1/"C"_"d"`
`= 1/8 + 1/8 + 1/8 = 3/8`
`"C"_"s" = 8/3` μF
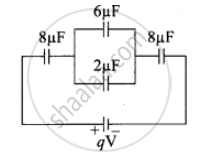
- Charge on each capacitor,
Charge on capacitor a, Qa = Cs V = `8/3 xx 9`
Qa = 24 μC
Charge on capacitor, d, Qd = Cs V = `8/3 xx 9`
Qd = 24 μC
Capacitor b and c in parallel
Charge on capacitor, b, Qb = `6/3 xx 9` = 18
Qb = 18 μC
Charge on capacitor, c, Qc = `2/3 xx 9` = 6
Qc = 6 μC - Potential difference across each capacitor, V = `"q"/"c"`
Capacitor Ca, Va = `"q"_"a"/"C"_"a" = (24 xx 10^6)/(8 xx 10^6)` = 3 V
Capacitor Cb, Vb = `"q"_"b"/"C"_"b" = (18 xx 10^6)/(6 xx 10^6)` = 3 V
Capacitor Cc, Vc = `"q"_"c"/"C"_"c" = (6 xx 10^6)/(2 xx 10^6)` = 3 V
Capacitor Cd, Vd = `"q"_"d"/"C"_"d" = (24 xx 10^6)/(8 xx 10^6)` = 3 V - Energy stores in a capacitor, U = `1/2` CV2
Energy in capacitor Ca, Ua = `1/2 "C"_"a" "V"_"a"^2 = 1/2 xx 8 xx 10^-6 xx (3)^2`
Ua = 36 μJ
Capacitor Cb, Ub = `1/2 "C"_"b" "V"_"b"^2 = 1/2 xx 6 xx 10^-6 xx (3)^2`
Ua = 27 μJ
Cc, Uc = `1/2 "C"_"c" "V"_"c"^2 = 1/2 xx 2 xx 10^-6 xx (3)^2`
Ua = 9 μJ
Cd, Ud = `1/2 "C"_"d" "V"_"d"^2 = 1/2 xx 8 xx 10^-6 xx (3)^2`
Ua = 36 μJ
APPEARS IN
संबंधित प्रश्न
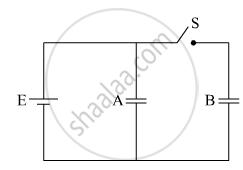
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
Two metal spheres of capacitance C1 and C2 carry some charges. They are put in contact and then separated. The final charges Q1 and Q2 on them will satisfy
Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
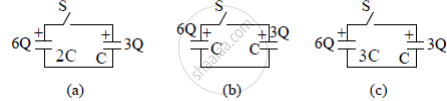
Three circuits, each consisting of a switch 'S' and two capacitors, are initially charged, as shown in the figure. After the switch has been closed, in which circuit will the charge on the left-hand capacitor
(i) increase,
(ii) decrease, and
(iii) remains the same? Give reasons.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
Calculate the resultant capacitances for each of the following combinations of capacitors.
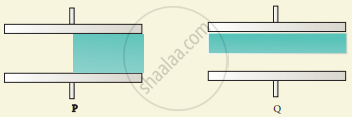
Capacitors P and Q have identical cross-sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant Er as shown in the figure. Calculate the capacitance of capacitors P and Q.
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.
The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.
The new capacitance (C') in terms of the original capacitance (C0) is given by the following relation:
Two plates A and B of a parallel plate capacitor are arranged in such a way, that the area of each plate is S = 5 × 10-3 m 2 and distance between them is d = 8.85 mm. Plate A has a positive charge q1 = 10-10 C and Plate B has charge q2 = + 2 × 10-10 C. Then the charge induced on the plate B due to the plate A be - (....... × 10-11 )C