Advertisements
Advertisements
प्रश्न
Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
उत्तर
We need to calculate the capacitance of an isolated charged sphere.
Let us assume that the charge on the sphere is Q and its radius is R.
Capacitance of the charged sphere can be found by imagining a concentric sphere of infinite radius consisting of −Q charge.
Potential difference between the spheres = `1/(4pi∈_0) Q/R` - 0 = `1/(4pi∈_0) Q/R`
Capacitance is the ratio of the magnitude of the charge on each conductor to the potential difference between them.
`C = Q/(1/(4pi∈_0) Q/R` = `4pi∈_0 R`
Therefore, the capacitances of spheres of radii R1 and R2 are C1 and C2, respectively. They are given by
`C_1 = 4pi∈_0 R_1`
`C_2 = 4pi∈_0 R_2`
If the spheres are connected by a metal wire, the charge will flow from one sphere to another till their potentials become the same.
As there potentials become the same, the potential difference between the conductors for both the capacitors also becomes the same. Thus, it can be concluded that the capacitors are connected in parallel.
Thus, the capacitance of the combination is given by `C_(eq) = C_1 + C_2`
= `4pi∈_0(R_1 + R_2)`
APPEARS IN
संबंधित प्रश्न
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
A capacitor has capacitance C. Is this information sufficient to know what maximum charge the capacitor can contain? If yes, what is this charges? If no, what other information is needed?
Find the charges on the three capacitors connected to a battery as shown in figure.
Take `C_1 = 2.0 uF , C_2 = 4.0 uF , C_3 = 6.0 uF and V` = 12 volts.

Take `C_1 = 4.0 "uF" and C_2 = 6.0 "uF"` in figure . Calculate the equivalent capacitance of the combination between the points indicated.

Find the charge supplied by the battery in the arrangement shown in figure.
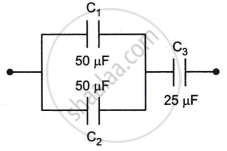
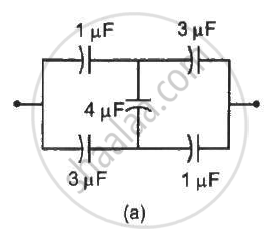
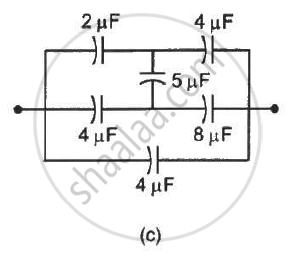
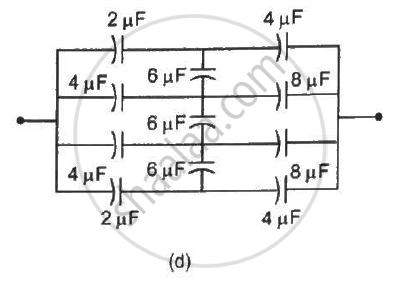
Find the equivalent capacitances of the combinations shown in figure between the indicated points.

A capacitor of capacitance 2⋅0 µF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4⋅0 µF as shown in figure . Find (a) the charge on each of the two capacitors after the connection, (b) the electrostatic energy stored in each of the two capacitors and (c) the heat produced during the charge transfer from one capacitor to the other.

The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
An air-filled parallel-plate capacitor is to be constructed which can store 12 µC of charge when operated at 1200 V. What can be the minimum plate area of the capacitor? The dielectric strength of air is `3 xx 10^6 "Vm"^-1`
Consider the situation shown in figure. The plates of the capacitor have plate area A and are clamped in the laboratory. The dielectric slab is released from rest with a length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period.
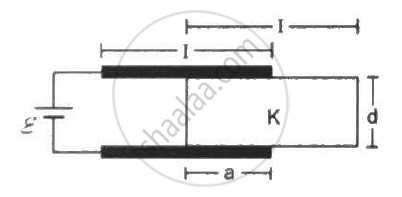
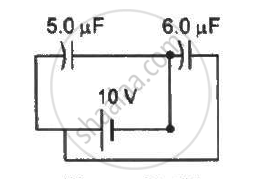
The figure show a network of five capacitors connected to a 10V battery. Calculate the charge acquired by the 5μF capacitor.
Obtain the expression for capacitance for a parallel plate capacitor.
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
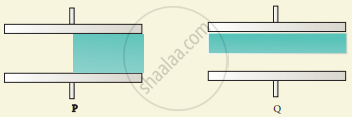
Capacitors P and Q have identical cross-sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant Er as shown in the figure. Calculate the capacitance of capacitors P and Q.
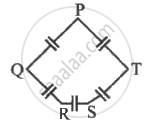
Five capacitor each of capacitance value C are connected as shown in the figure. The ratio of capacitance between P to R, and the capacitance between P and Q is ______.
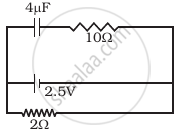
A capacitor of 4 µ F is connected as shown in the circuit (Figure). The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be ______.
A 5µF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 µF capacitor If the energy change during the charge redistribution is `"X"/100`J then value of X to the 100 nearest integer is ______.
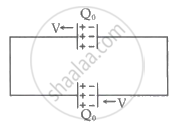
Two identical capacitors are connected as shown and have an initial charge of Q0. The separation between the plates of each capacitor is d0. Suddenly the left plate of the upper capacitor and right plate of the lower capacitor start moving with speed v towards the left while the other plate of each capacitor remains fixed. `("given" (Q_0V)/(2d_0) = 10 A)`. The value of current in the circuit is ______ A.
A capacitor with capacitance 5µF is charged to 5 µC. If the plates are pulled apart to reduce the capacitance to 2 µF, how much work is done?
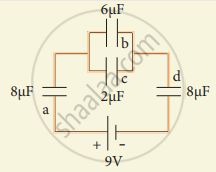
Calculate equivalent capacitance of the circuit shown in the Figure given below: