Advertisements
Advertisements
प्रश्न
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
उत्तर
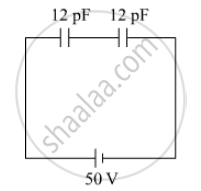
Series combination
In series combination, Equivalent capacitance, Ceq would be given as
`C_"eq"= (C_1C_2)/(C_1+C_2)`
`= (12×12)/(12+12)`
`= 6 pF`
Electrostatic energy stored in the series combination would be
=`12C_"eq"V^2 `
`= 12×6×10^-12×50^2`
`= 7.5×10^-9 "Joule"`.
Charge drawn from battery in series combination,
`Q = C_"eq"V`
`= 6×10^-12×50`
`= 3×10^-10 C`
APPEARS IN
संबंधित प्रश्न
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
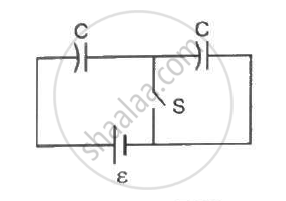
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
Consider an assembly of three conducting concentric spherical shell of radii a, b and c as shown in figure Find the capacitance of the assembly between the points Aand B.

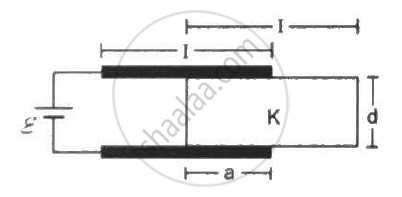
Consider the situation shown in figure. The plates of the capacitor have plate area A and are clamped in the laboratory. The dielectric slab is released from rest with a length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period.
Derive the expression for resultant capacitance, when the capacitor is connected in parallel.
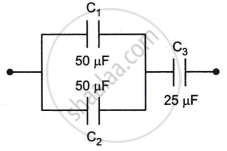
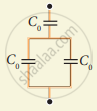
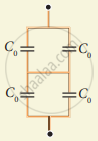
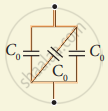
Calculate the resultant capacitances for each of the following combinations of capacitors.
Consider two conducting spheres of radii R1 and R2 with R1 > R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
Obtain the equivalent capacitance of the network shown in the figure. For a 300 V supply, determine the charge on each capacitor.
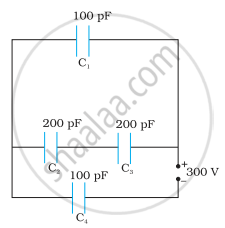
Calculate equivalent capacitance of the circuit shown in the Figure given below: