Question

Derive the mirror equation and the equation for lateral magnification.

Answer 1

1. The mirror equation establishes a relation among object distance u, image distance v and focal length/for a spherical mirror. An object AB is considered on the principal axis of a concave mirror beyond the center of curvature C’.
2. Let us consider three paraxial rays from point B on the object.
3. The first paraxial ray BD travelling parallel to the principal axis is incident on the concave mirror at D, close to the pole P. After reflection the ray passes through the focus F. The second paraxial ray BP incident at pole P is reflected along PBThe third paraxial ray BC passing through centre of curvature C, falls normally on the mirror at E is reflected back along the same path.
4. The three reflected rays intersect at point B’. A perpendicular drawn as A’ B’ to the principal axis is the real, inverted image of the object AB.
   
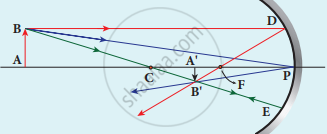
   Mirror equation
5. As per law of reflection, the angle of incidence ∠BPA is equal to the angle of reflection ∠B’PA’. The triangles ∆BPA and ∆B’PA’ are similar. Thus, from the rule of similar triangles,
   `("A'""B'")/"AB" = "PA'"/"PA"`  .....(1)
   The other set of similar triangles are, ADPF and A BA.’ F. (PD is almost a straight vertical line)
   `("A'""B'")/"PD" = "AF'"/"PF"`
   As, the distances PD = AB the above equation becomes,
   `("A'""B'")/"AB" = "AF'"/"PF"`   ....(2)
   From equations (1) and (2) we can write,
   `"PA'"/"PA" = "AF'"/"PF"`
   As, A’ F = PA’ – PF, the above equation becomes,
   `"PA'"/"PA" = ("PA'" - "PF'""P")/"PF"`   .....(3)
   We can apply the sign conventions for the various distances in the above equation.
   PA = – u, PA’ = -v, PF = -f
   All three distances are negative as per sign convention because they are measured to the left of the pole. Now, the equation (3) becomes,
   `(-"v")/(-"u") = (- "v"(- "f"))/(- "f")`
   On further simplification,
   `(-"v")/(-"u") = ("v - f")/"f"; "v"/"u" = "v"/"f" = 1`
   Dividing either side with v,
   `1/"u" = 1/"f" = 1/"v"`
   After rearranging,
   `1/"v" + 1/"u" = 1/"f"`   ....(4)
   

   The above equation (4) is called mirror equation.

6. Lateral magnification in spherical mirrors:
   The lateral or transverse magnification is defined as the ratio of the height of the image to the height of the object. The height of the object and image are measured perpendicular to the principal axis.
   magnification (m) = `"height of the image (h')"/"height of the object (h)"`
   m = `("h'")/"h"`    ....(5)
   Applying proper sign conventions for equation (1),
   `("A'""B'")/"AB" = "PA'"/"PA"`
   A’B’ = -h, AB = h, PA’ = -v, PA = -u
   `(-"h'")/"h" = (- "v")/(- "u")`
   On simplifying we get,
   m = `"h'"/"h" = - "v"/"u"`   ....(6)
   Using mirror equation, we can further write the magnification as,
   m = `("h'")/"h" - ("f - v")/"f" = "f"/("f - u")`   ....(7)