Advertisements
Advertisements
Question
Describe briefly Davisson – Germer experiment which demonstrated the wave nature of electrons.
Solution
Davisson – Germer experiment:
1. De Broglie's hypothesis of matter waves was experimentally confirmed by Clinton Davisson and Lester Germer in 1927. They demonstrated that electron beams are diffracted when they fall on crystalline solids.
2. Since a crystal can act as a three-dimensional diffraction grating for matter waves, the electron waves incident on crystals are diffracted off in certain specific directions.

Experimental set up of Davisson – Germer experiment
3. The filament F is heated by a low tension (L.T.) battery. Electrons are emitted from the hot filament by thermionic emission. They are then accelerated due to the potential difference between the filament and the anode aluminium cylinder by a high tension (H.T.) battery.
4. Electron beam is collimated by using two thin aluminium diaphragms and is allowed to strike a single crystal of Nickel.
5. The electrons scattered by Ni atoms in different directions are received by the electron detector which measures the intensity of the scattered electron beam.
6. The detector is rotatable in the plane of the paper so that the angle θ between the incident beam and the scattered beam can be changed at our will.
7. The intensity of the scattered electron beam is measured as a function of the angle θ.
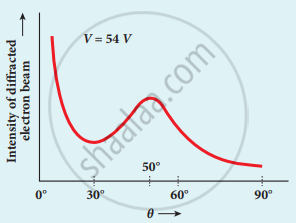
Variation of intensity of diffracted electron beam with the angle θ
8. From the graph shows the variation of intensity of the scattered electrons with the angle θ for the accelerating voltage of 54 V. For a given accelerating voltage V, the scattered wave shows a peak or maximum at an angle of 50° to the incident electron beam.
This peak in intensity is attributed to the constructive interference of electrons diffracted from various atomic layers of the target material.
9. From the known value of interplanar spacing of Nickel, the wavelength of the electron wave has been experimentally calculated as 1.65 Å.
10. The wavelength can also be calculated from de Broglie's relation for V = 54 V from the equation.
λ = `12.27/sqrt"V"` Å = `12.27/sqrt54` Å
λ = 1.67 Å
11. This value agrees well with the experimentally observed wavelength of 1.65 Å. Thus this experiment directly verifies de Broglie’s hypothesis of the wave nature of moving particles.
APPEARS IN
RELATED QUESTIONS
State de Broglie hypothesis.
Why we do not see the wave properties of a baseball?
A proton and an electron have the same kinetic energy. Which one has a greater de Broglie wavelength? Justify.
Write the relationship of de Broglie wavelength λ associated with a particle of mass m in terms of its kinetic energy K.
An electron and an alpha particle have the same kinetic energy. How are the de Broglie wavelengths associated with them related?
Derive an expression for de Broglie wavelength of electrons.
Briefly explain the principle and working of electron microscope.
Calculate the de Broglie wavelength of a proton whose kinetic energy is equal to 81.9 × 10–15 J.
(Given: mass of proton is 1836 times that of electron).
A deuteron and an alpha particle are accelerated with the same potential. Which one of the two has
- greater value of de Broglie wavelength associated with it and
- less kinetic energy?
Explain.
An electron is accelerated through a potential difference of 81 V. What is the de Broglie wavelength associated with it? To which part of the electromagnetic spectrum does this wavelength correspond?
