Question

Describe the construction and working of venturimeter and obtain an equation for the volume of liquid flowing per second through a wider entry of the tube.

Answer 1

Construction: It consists of two wider tubes A and A’ (with cross-sectional area A) connected by a narrow tube B (with the cross-sectional area a). A manometer in the form of a U-tube is also attached between the wide and narrow tubes as shown in Figure. The manometer contains a liquid of density ‘ρ_m‘.

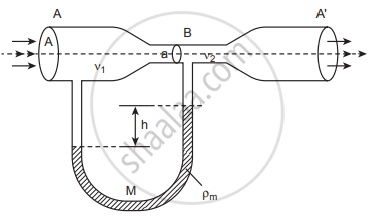
           A schematic diagram of venturimeter

Theory: Let P₁ be the pressure of the fluid at the wider region of tube A. Let us assume that the fluid of density ‘ρ’ flows from the pipe with speed ‘v₁’ and into the narrow region, its speed increases to ‘v₂‘.

According to Bernoulli’s equation, this increase in speed is accompanied by a decrease in the fluid pressure P₂ at the narrow region of tube B. Hence, the pressure difference between tubes A and B is noted by measuring the height difference (∆P = P₁ – P₂) between the surfaces of the manometer liquid.

From the equation of continuity, we can say that Av₁ = av₂ which means that

v₂ = `"A"/"a" "v"_1`

Using Bernoulli’s equation,

`"P"_1 + ρ "v"_1^2/2 = "P"_2 + ρ "V"_2^2/2 = "P"_2 + ρ1/2("A"/"a" "v"_1)^2`

From the above equation, the pressure difference

ΔP = P₁ − P₂ = `ρ "v"_1^2/2 (("A"^2 - "a"^2))/"a"^2`

Thus, the speed of flow of fluid at the wide end of the tube A

`"v"_1^2 = (2(Δ"P")"a"^2)/(ρ("A"^2 - "a"^2)) ⇒ "v"_1 = sqrt((2(Δ"P")"a"^2)/(ρ("A"^2 - "a"^2))`

The volume of the liquid flowing out per second is

V = `"Av"_1 = "A" sqrt((2(Δ"P")"a"^2)/(ρ("A"^2 - "a"^2))) = "aA" = sqrt((2(Δ"P"))/(ρ("A"^2 - "a"^2))`