Advertisements
Advertisements
Question
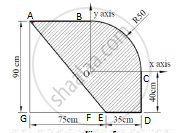
Determine the position of the centroid of the plane lamina. Shaded portion is removed.
Short Note
Solution
| FIGURE | AREA (mm2) |
X co-ordinate Of centroid (mm) |
Y co-ordinate Of centroid (mm) | Ax (mm2) | Ay (mm2) |
| Rectangle | 120 x 100 =12000 | `120/2=60` | `120/2=60` | 720000 | 600000 |
| Triangle | `1/2`120 x 60 =3600 | `120/3=40` | `-60/2=60` | 144000 | -72000 |
| Semicircle | `1/2`𝝅 x 602 =1800 𝝅 =5654.8668 |
`120/2=60` | `100+(4∗60)/(3x)` =125.4648 |
339292.01 | 709486.68 |
| Circle (Removed) |
- 𝝅 x 402 =5026.5482 |
`120/2=60` | 100 | -301592.89 | -502654.82 |
| Total | 16228.32 | 901699.12 | 734831.86 |
`(Σ Ax)/(Σ A)=(901699.12)/(16228.32)= 55.56 mm`
`(Σ Ay)/(Σ A)=(734831.86)/(16228.32)= 45.28 mm`
Centroid is at (55.56,45.28)mm
shaalaa.com
Centroid for Plane Laminas
Is there an error in this question or solution?