Advertisements
Advertisements
Question
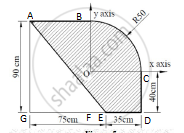
For the composite lamina shown in the figure, determine the coordinates of its centroid.
Answer in Brief
Solution
Area of the shaded region = Rectangle ABFG + Rectangle OCDF + Quarter Circle OCB – Triangle AEG
| Figure | Area | x coordinate | y coordinate | Aixi | Aiyi |
| Rectangle ABFG |
90 x 60 = 5400 mm2 |
`(-60)/2 = - 30` | `50-90/2 =5` | -162000 | 27000 |
| Rectangle OCDF |
40 x 50 = 2000 mm2 |
`50/2 = 25` | `-40/2`=-20` | 50000 | -40000 |
| Quarter Circle OCB |
`1/4 xx pi xx 50^2= 1963.495 mm^2` | 21.22 | 21.22 | 41665.3639 | 41665.3639 |
| Triangle AEG |
`-1/2 xx 75 xx 90 = 3375 mm ^2` | -35 | -10 | 118125 |
33750
|
ΣAi = 5400 + 2000 + 1963.495 – 3375 = 5988.495
ΣAixi = -162000 + 50000 + 41665.3639 + 118125 = 47790.3639
ΣAiyi = 27000 - 40000 + 41665.3639 + 33750 = 62415.3639
`overlineX = (ΣAix i)/(ΣAi) =(3790.3639)/5988.495 = 7.98m`
`overlineY = = (ΣAix i)/(ΣAi) = 10.423m`
Coordinates of centroid are (7.98,10.423).
shaalaa.com
Centroid for Plane Laminas
Is there an error in this question or solution?


