Advertisements
Advertisements
Question
Replace the force system shown in Figure 6 with a single force and couple system acting at point B.
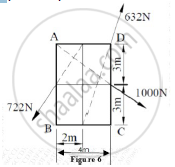
Answer in Brief
Solution
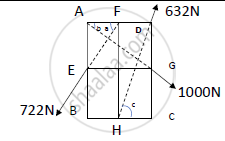
| `(In DeltaAGF) b=tan^(-1) (GD)/(DA) = tan ^(-1) 3/4 = 36.87°` | `(In DeltaAEF) a = tan ^ (-1) (AE)/(AF) = tan^(-1) 3/2 = 56.32°|` | `(InDeltaFHD)C = tan^(-1) (DC)/(CH) = tan ^(-1) 6/2 =71.57° ` |
ΣFx = 1000cos(36.87) + 632cos(71.57) – 722cos(56.32) = 599.42
ΣFy = - 1000sin(36.87) + 632sin(71.57) – 722sin(56.32) = -601.23
`R = sqrt(Fx^2 +FY^2)`
`R = sqrt(599.42^2 +(-601.23)^2)`
`R = 848.99 N`
`Theta = tan^(-1) ((Sigma Fy)/(SigmaFx))`
`= tan^(-1) ((-601.23)/(599.42))`
= -45.0860
`ΣM_(B^F) `= - [722cos(56.32)x3] + [1000cos(36.87)x6] – [632sin(71.57)x2]
`ΣM_(B^F)` = 2399.66 N-m
The magnitudes of the resultant force and couple at B are 848.99 N and 2399.66 N-m clockwise.
shaalaa.com
Resultant of Concurrent Force System
Is there an error in this question or solution?
