Advertisements
Advertisements
Question
Determine the required stiffness k so that the uniform 7 kg bar AC is in equilibrium when θ=30o.
Due to the collar guide at B the spring remains vertical and is unstretched when θ = 0o.Use principle of virtual work.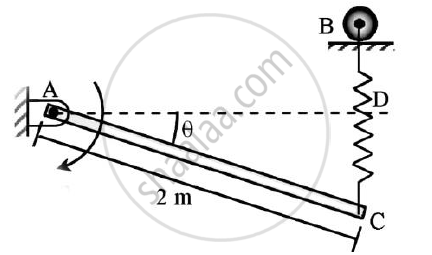
Solution
Solution:
Given : : Mass of bar AC = 7 kg
θ = 30°
To find : Required stiffness k
Solution:
Weight of rod = 7g N
Assume rod AC have a small virtual angular displacement 𝛿θ in anti-clockwise direction
Reaction forces HA and VA do not do any virtual work
Un-stretched length of the spring = BD
Extension of the spring (x) = CD = 2sin θ
Assume FS be the spring force at end C of the rod
FS = Kx = 2Ksin θ
Assume A to be the origin and AD be the X-axis of the system
| Active force | Co-ordinate of the point of action along the force | Virtual Displacement |
| W=7g | -sin θ | 𝛿yM=-cos θ 𝛿 θ |
| FS=2Ksin θ | -2sin θ | 𝛿yC’=-2cos θ 𝛿 θ |
APPLYING PRINCIPLE OF VIRTUAL WORK
𝛿U = 0
-W X 𝛿YM + FS X 𝛿YC’ + 50 X 𝛿 θ = 0
2Ksin θ x (-2cos θ 𝛿 θ) = 7g x (-cos θ 𝛿 θ) - 50 x 𝛿 θ
Substituting the value of θ and solving
K=63.2025 Nm
The required stiffness K for bar AC to remain in equilibrium is 63.2025 Nm
APPEARS IN
RELATED QUESTIONS
Determine the tension in a cable BC shown in fig by virtual work method.

Given: F=3500 N
ϴ = 50o
Length of rod = 3.75 mm + 1.5 mm = 5.25 mm
To find : Tension in cable BC
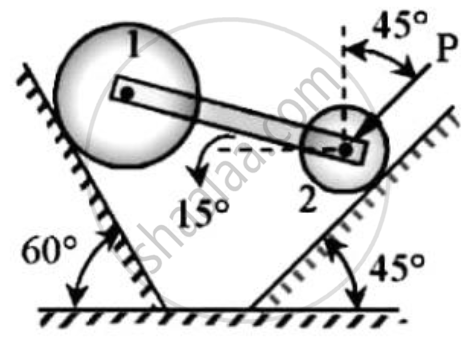
Two cylinders 1 and 2 are connected by a rigid bar of negligible weight hinged to each cylinder and left to rest in equilibrium in the position shown under the application of force P applied at the center of cylinder 2.
Determine the magnitude of force P.If the weights of the cylinders 1 and 2 are 100N and 50 N respectively.
Using Principle of Virtual Work, determine the force P which will keep the weightless bar AB in equilibrium. Take length AB as 2m and length AC as 8m. The bar makes an angle of 30° with horizontal. All the surfaces in contact are smooth. Refer Figure 9.