Advertisements
Advertisements
Question
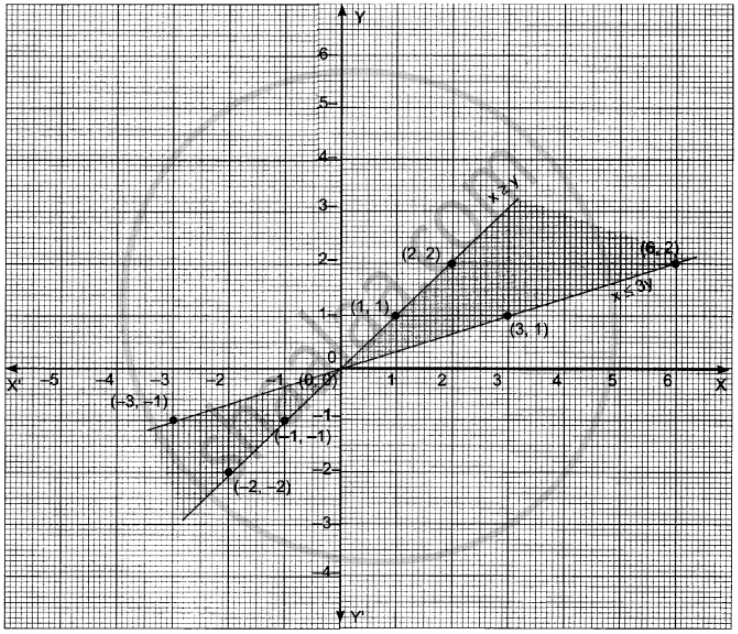
Determine the region in the plane determined by the inequalities:
x ≤ 3y, x ≥ y
Solution
Given in equation are x ≤ 3y, x ≥ y
Suppose x = 3y
⇒`x/3` = y
| x | 0 | 3 | 6 | – 3 |
| y | 0 | 1 | 2 | – 1 |
If x = y
| x | 1 | 2 | – 1 | – 2 |
| y | 1 | 2 | – 1 | – 2 |
APPEARS IN
RELATED QUESTIONS
Find all values of x for which `(x^3(x - 1))/((x - 2)) > 0`
Solve `(x^2 - 4)/(x^2 - 2x - 15) ≤ 0`
Resolve the following rational expressions into partial fractions
`(3x + 1)/((x - 2)(x + 1))`
Resolve the following rational expressions into partial fractions
`x/((x - 1)^3`
Resolve the following rational expressions into partial fractions
`(x - 1)^2/(x^3 + x)`
Resolve the following rational expressions into partial fractions
`(x^2 + x + 1)/(x^2 - 5x + 6)`
Resolve the following rational expressions into partial fractions
`(x^3 + 2x + 1)/(x^2 + 5x + 6)`
Resolve the following rational expressions into partial fractions
`(x + 12)/((x + 1)^2 (x - 2))`
Resolve the following rational expressions into partial fractions
`(6x^2 - x + 1)/(x^3 + x^2 + x + 1)`
Resolve the following rational expressions into partial fractions
`(7 + x)/((1 + x)(1 + x^2))`
Determine the region in the plane determined by the inequalities:
y ≥ 2x, −2x + 3y ≤ 6
Determine the region in the plane determined by the inequalities:
3x + 5y ≥ 45, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 35, y ≥ 2, x ≥ 5.
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0
Choose the correct alternative:
The solution of 5x − 1 < 24 and 5x + 1 > −24 is
Choose the correct alternative:
The solution set of the following inequality |x − 1| ≥ |x − 3| is
