Advertisements
Advertisements
Question
Determine whether the following function is differentiable at the indicated values.
f(x) = |x2 – 1| at x = 1
Solution
`f(x) = {{:(-(x^2 - 1), "if" x < 1),(x^2 - 1, "if" x> 1):}`
To find the left limit of f(x) at x = 1
When x → `1^-`
f(x) = `-(x^2 - 1)`
`f"'"(1^-) = lim_(x -> 1^-) (f(x) - f(1))/(x - 1)`
= `lim_(x -> 1^-) (-(x^2 - 1) - [-(1^2 - 1)])/(x - 1)`
= `lim_(x - 1^-) (-(x^2 - 1) - 0)/(x - 1)`
= `lim_(x -> 1^-) (-(x - 1)(x + 1))/(x - 1)`
= `lim_(x -> 1^-) - (x + 1)`
`f"'"(1^-) = -(1 + 1)` = – 2 ........(1)
To find the right limit of f(x) at x = 1
When x → `1^+`
f(x) = `(x^2 - 1)`
`f"'"(1^+) = lim_(x -> 1^+) (f(x) - f(1))/(x - 1)`
= `lim_(x -> 1^+) ((x^2 - 1) - (1^2 - 1))/(x - 1)`
= `lim_(x - 1^+) ((x^2 - 1) - 0)/(x - 1)`
= `lim_(x -> 1^+) ((x - 1)(x + 1))/(x - 1)`
= `lim_(x -> 1^+) (x + 1)`
`f"'"(1^+) = (1 + 1)` = 2 ........(2)
From equatios (1) and (2) we have
`f"'"(1^+) ≠ f"'"(1^+)`
∴ f(x) is not differentiable at x = 1.
APPEARS IN
RELATED QUESTIONS
Find the derivatives of the following functions using first principle.
f(x) = 6
Find the derivatives of the following functions using first principle.
f(x) = – 4x + 7
Find the derivatives of the following functions using first principle.
f(x) = – x2 + 2
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = sqrt(1 - x^2)`
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = {{:(x",", x ≤ 1),(x^2",", x > 1):}`
Determine whether the following function is differentiable at the indicated values.
f(x) = |x| + |x – 1| at x = 0, 1
Determine whether the following function is differentiable at the indicated values.
f(x) = sin |x| at x = 0
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.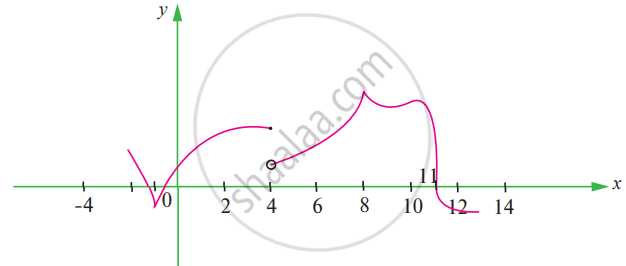
If f(x) = |x + 100| + x2, test whether f’(–100) exists.
Examine the differentiability of functions in R by drawing the diagram
|sin x|
Examine the differentiability of functions in R by drawing the diagram
|cos x|
Choose the correct alternative:
If f(x) = x2 – 3x, then the points at which f(x) = f’(x) are
Choose the correct alternative:
If y = mx + c and f(0) = f’(0) = 1, then f(2) is
Choose the correct alternative:
If f(x) = x + 2, then f'(f(x)) at x = 4 is
Choose the correct alternative:
If pv = 81, then `"dp"/"dv"` at v = 9 is
Choose the correct alternative:
It is given that f'(a) exists, then `lim_(x -> "a") (xf("a") - "a"f(x))/(x - "a")` is
Choose the correct alternative:
If f(x) = `{{:(x + 2, - 1 < x < 3),(5, x = 3),(8 - x, x > 3):}` , then at x = 3, f'(x) is
