Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 10 - Differential Calculus - Differentiability and Methods of Differentiation [Latest edition]

Find the derivatives of the following functions using first principle.

f(x) = 6

Find the derivatives of the following functions using first principle.

f(x) = – 4x + 7

Find the derivatives of the following functions using first principle.

f(x) = – x² + 2

Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

`f(x) = |x - 1|`

Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

`f(x) = sqrt(1 - x^2)`

Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

`f(x) = {{:(x",", x ≤ 1),(x^2",", x > 1):}`

Determine whether the following function is differentiable at the indicated values.

f(x) = x |x| at x = 0

Determine whether the following function is differentiable at the indicated values.

f(x) = |x² – 1| at x = 1

Determine whether the following function is differentiable at the indicated values.

f(x) = |x| + |x – 1| at x = 0, 1

Determine whether the following function is differentiable at the indicated values.

f(x) = sin |x| at x = 0

Show that the following functions are not differentiable at the indicated value of x.

`f(x) = {{:(-x + 2, x ≤ 2),(2x - 4, x > 2):}` , x = 2

Show that the following functions are not differentiable at the indicated value of x.

`f(x) = {{:(3x",", x < 0),(-4x",", x ≥ 0):}` , x = 0

The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.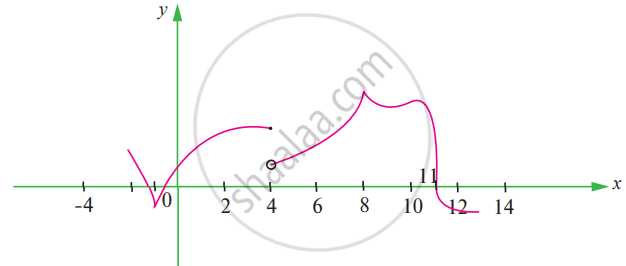

If f(x) = |x + 100| + x², test whether f’(–100) exists.

Examine the differentiability of functions in R by drawing the diagram

|sin x|

Examine the differentiability of functions in R by drawing the diagram

|cos x|

Find the derivatives of the following functions with respect to corresponding independent variables:

f(x) = x – 3 sin x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = sin x + cos x

Find the derivatives of the following functions with respect to corresponding independent variables:

f(x) = x sin x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = cos x – 2 tan x

Find the derivatives of the following functions with respect to corresponding independent variables:

g(t) = t³ cos t

Find the derivatives of the following functions with respect to corresponding independent variables:

g(t) = 4 sec t + tan t

Find the derivatives of the following functions with respect to corresponding independent variables:

y = e^x sin x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = `tan x/x`

Find the derivatives of the following functions with respect to corresponding independent variables:

y = `sinx/(1 + cosx)`

Find the derivatives of the following functions with respect to corresponding independent variables:

y = `x/(sin x + cosx)`

Find the derivatives of the following functions with respect to corresponding independent variables:

y = `(tanx - 1)/secx`

Find the derivatives of the following functions with respect to corresponding independent variables:

y = `sinx/x^2`

Find the derivatives of the following functions with respect to corresponding independent variables:

y = tan θ (sin θ + cos θ)

Find the derivatives of the following functions with respect to corresponding independent variables:

y = cosec x . cot x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = x sin x cos x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = e^-x . log x

Find the derivatives of the following functions with respect to corresponding independent variables:

y = (x² + 5) log(1 + x) e^–3x 

Find the derivatives of the following functions with respect to corresponding independent variables:

y = sin x⁰ 

Find the derivatives of the following functions with respect to corresponding independent variables:

y = log₁₀ x

Find the derivatives of the following functions with respect to corresponding independent variables:

Draw the function f'(x) if f(x) = 2x² – 5x + 3

Differentiate the following:
y = (x² + 4x + 6)⁵

Differentiate the following:
y = tan 3x

Differentiate the following:
y = cos (tan x)

Differentiate the following:
y = `root(3)(1 + x^3)`

Differentiate the following:
y = `"e"^sqrt(x)`

Differentiate the following:
y = sin (e^x)

Differentiate the following:
F(x) = (x³ + 4x)⁷

Differentiate the following:

h(t) = `("t" - 1/"t")^(3/2)`

Differentiate the following:

f(t) = `root(3)(1 + tan "t")`

Differentiate the following:
y = cos (a³ + x³)

Differentiate the following:
y = e^–mx 

Differentiate the following:
y = 4 sec 5x

Differentiate the following:
y = (2x – 5)⁴ (8x² – 5)^–3 

Differentiate the following:

y = `(x^2 + 1) root(3)(x^2 + 2)`

Differentiate the following:

y = `x"e"^(-x^2)`

Differentiate the following:

s(t) = `root(4)(("t"^3 + 1)/("t"^3 - 1)`

Differentiate the following:

f(x) = `x/sqrt(7 - 3x)`

Differentiate the following:
y = tan (cos x)

Differentiate the following:

y = `(sin^2x)/cos x`

Differentiate the following:

y = `5^((-1)/x)`

Differentiate the following:
y = `sqrt(1 + 2tanx)`

Differentiate the following:
y = sin³x + cos³x

Differentiate the following:
y = sin²(cos kx)

Differentiate the following:
y = (1 + cos²)⁶

Differentiate the following:

y = `"e"^(3x)/(1 + "e"^x`

Differentiate the following:
y = `sqrt(x +sqrt(x)`

Differentiate the following:
y = `"e"^(xcosx)`

Differentiate the following:
y = `sqrt(x + sqrt(x + sqrt(x)`

Differentiate the following:
y = `sin(tan(sqrt(sinx)))`

Differentiate the following:

y = `sin^-1 ((1 - x^2)/(1 + x^2))`

Find the derivatives of the following:
y = `x^(cosx)`

Find the derivatives of the following:
y = `x^(logx) + (logx)^x`

Find the derivatives of the following:
`sqrt(x) = "e"^((x - y))`

Find the derivatives of the following:
x^y = y^x

Find the derivatives of the following:
(cos x)^{log x}

Find the derivatives of the following:

`x^2/"a"^2 + y^2/"b"^2` = 1

Find the derivatives of the following:

`sqrt(x^2 + y^2) = tan^-1 (y/x)`

Find the derivatives of the following:
tan (x + y) + tan (x – y) = x

Find the derivatives of the following:

If cos(xy) = x, show that `(-(1 + ysin(xy)))/(xsiny)`

Find the derivatives of the following:

`tan^-1sqrt((1 - cos x)/(1 + cos x)` 

Find the derivatives of the following:

`tan^-1 = ((6x)/(1 - 9x^2))`

Find the derivatives of the following:

`cos[2tan^-1 sqrt((1 - x)/(1 + x))]`

Find the derivatives of the following:

x = `"a" cos^3"t"` ; y = `"a" sin^3"t"`

Find the derivatives of the following:

x = a (cos t + t sin t); y = a (sin t – t cos t)

Find the derivatives of the following:

x = `(1 - "t"^2)/(1 + "t"^2)`, y = `(2"t")/(1 + "t"^2)`

Find the derivatives of the following:

`cos^-1 ((1 - x^2)/(1 + x^2))`

Find the derivatives of the following:

sin^-1 (3x – 4x³)

Find the derivatives of the following:

`tan^-1 ((cos x + sin x)/(cos x - sin x))`

Find the derivatives of the following:

Find the derivative of sin x² with respect to x² 

Find the derivatives of the following:

Find the derivative of `sin^-1 ((2x)/(1 + x^2))` with respect to `tan^-1 x`

Find the derivatives of the following:

If u = `tan^-1  (sqrt(1 + x^2) - 1)/x` and v = `tan^-1 x`, find `("d"u)/("d"v)`

Find the derivatives of the following:

Find the derivative with `tan^-1 ((sinx)/(1 + cos x))` with respect to `tan^-1 ((cosx)/(1 + sinx))`

Find the derivatives of the following:

If y = sin^–1x then find y”

Find the derivatives of the following:

If y = e^tan–1x, show that (1 + x²)y” + (2x – 1)y’ = 0

Find the derivatives of the following:

If y = `(sin^-1 x)/sqrt(1 - x^2)`, show that (1 – x²)y₂ – 3xy₁ – y = 0

Find the derivatives of the following:

If x = a(θ + sin θ), y = a(1 – cos θ) then prove that at θ = `pi/2`, yⁿ = `1/"a"`

Find the derivatives of the following:

If sin y = x sin(a + y), the prove that `("d"y)/("d"x) = (sin^2("a" + y))/sin"a"`, a ≠ nπ

Find the derivatives of the following:

If y = `(cos^-1 x)^2`, prove that `(1 - x^2) ("d"^2y)/("d"x)^2 - x ("d"y)/("d"x) - 2` = 0. Hence find y₂ when x = 0

Choose the correct alternative:

`"d"/("d"x) (2/pi sin x^circ)` is

Choose the correct alternative:

f y = f(x² + 2) and f'(3) = 5 , then `("d"y)/("d"x)` at x = 1 is

Choose the correct alternative:

If y = `1/4 u^4`, u = `2/3 x^3 + 5`, then `("d"y)/("d"x)` is 

Choose the correct alternative:

If f(x) = x² – 3x, then the points at which f(x) = f’(x) are

Choose the correct alternative:

If y = `1/("a" - z)`, then `("d"z)/("d"y)` is

Choose the correct alternative:

If y = cos (sin x²), then `("d"y)/("d"x)` at x = `sqrt(pi/2)` is

Choose the correct alternative:

If y = mx + c and f(0) = f’(0) = 1, then f(2) is

Choose the correct alternative:
If f(x) = x tan^-1x then f'(1) is

Choose the correct alternative:

`"d"/("d"x) ("e"^(x + 5log x))` is

Choose the correct alternative:

If the derivative of (ax – 5)e^3x at x = 0 is – 13, then the value of a is

Choose the correct alternative:

x = `(1 - "t"^2)/(1 + "t"^2)`, y = `(2"t")/(1 + "t"^2)` then `("d"y)/("d"x)` is

Choose the correct alternative:

If x = a sin θ and y = b cos θ, then `("d"^2y)/("d"x^2)` is

Choose the correct alternative:

The differential coefficient of `log_10 x` with respect to `log_x 10` is

Choose the correct alternative:

If f(x) = x + 2, then f'(f(x)) at x = 4 is

Choose the correct alternative:

If y = `(1 - x)^2/x^2`, then `("d"y)/("d"x)` is

Choose the correct alternative:

If pv = 81, then `"dp"/"dv"` at v = 9 is

Choose the correct alternative:

If f(x) = `{{:(x - 5,  "if"  x ≤ 1),(4x^2 - 9,  "if"  1 < x < 2),(3x + 4,  "if"  x ≥ 2):}` , then the right hand derivative of f(x) at x = 2 is

Choose the correct alternative:

It is given that f'(a) exists, then `lim_(x -> "a") (xf("a") - "a"f(x))/(x - "a")` is

Choose the correct alternative:

If f(x) = `{{:(x + 1,  "when"   x < 2),(2x - 1,  "when"  x ≥ 2):}` , then f'(2) is

Choose the correct alternative:

If g(x) = (x² + 2x + 1) f(x) and f(0) = 5 and `lim_(x -> 0) (f(x) - 5)/x` = 4, then g'(0) is

Choose the correct alternative:

If f(x) = `{{:(x + 2, - 1 < x < 3),(5, x = 3),(8 - x, x > 3):}` , then at x = 3, f'(x) is

Choose the correct alternative:

The derivative of f(x)= x|x| at x = – 3 is

Choose the correct alternative:

If f(x) = `{{:(2"a" - x,  "for"  - "a" < x < "a"),(3x - 2"a", "for"  x ≥ "a"):}` , then which one of the following is true?

Choose the correct alternative:

If f(x) = `{{:("a"x^2 - "b"",", - 1 < x < 1),(1/|x|",",  "elsewhere"):}` is differentiable at x = 1, then

Choose the correct alternative:

The number of points in R in which the function f(x) = |x – 1| + |x – 3| + sin x is not differentiable, is