Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 1 - Sets, Relations and Functions [Latest edition]

Write the following in roaster form.

{x ∈ N : x² < 121 and x is a prime}

Write the following in roster form.

The set of all positive roots of the equation (x − 1)(x + 1)(x² − 1) = 0

Write the following in roster form

{x ∈ N : 4x + 9 < 52}

Write the following in roster form.

{x : `(x − 4)/(x + 2)` = 3, x ∈ R – {– 2}}

Write the set {−1, 1} in set builder form

State whether the following set are finite or infinite.

{x ∈ N : x is an even prime number}

State whether the following set are finite or infinite.

{x ∈ N : x is an odd prime number}

State whether the following set are finite or infinite.

{x ∈ Z : x is even and less than 10}

State whether the following set are finite or infinite.

{x ∈ R : x is a rational number}

State whether the following set are finite or infinite.

{x ∈ N : x is a rational number}

By taking suitable sets A, B, C, verify the following results:

A × (B ∩ C) = (A × B) ∩ (A × C)

By taking suitable sets A, B, C, verify the following results:

A × (B ∪ C) = (A × B) ∪ (A × C)

By taking suitable sets A, B, C, verify the following results:

(A × B) ∩ (B × A) = (A ∩ B) × (B ∩ A)

By taking suitable sets A, B, C, verify the following results:

C − (B − A) = (C ∩ A) ∪ (C ∩ B')

By taking suitable sets A, B, C, verify the following results:

(B − A) ∩ C = (B ∩ C) − A = B ∩ (C − A)

By taking suitable sets A, B, C, verify the following results:

(B − A) ∪ C = (B ∪ C) − (A − C)

Justify the trueness of the statement:
“An element of a set can never be a subset of itself.”

If n(P(A)) = 1024, n(A ∪ B) = 15 and n(P(B)) = 32, then find n(A ∩ B)

If n (A ∩ B) = 3 and n(A ∪ B) = 10, then find n(P(A ∆ B))

For a set A, A × A contains 16 elements and two of its elements are (1, 3) and (0, 2). Find the elements of A

Let A and B be two sets such that n (A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y, z are distinct elements

If A × A has 16 elements, S = {(a, b) ∈ A × A : a < b} ; (−1, 2) and (0, 1) are two elements of S, then find the remaining elements of S

Discuss the following relation for reflexivity, symmetricity and transitivity:

The relation R defined on the set of all positive integers by “mRn if m divides n”

Discuss the following relation for reflexivity, symmetricity and transitivity:

Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”

Discuss the following relation for reflexivity, symmetricity and transitivity:

Let A be the set consisting of all the members of a family. The relation R defined by “aRb if a is not a sister of b”

Discuss the following relation for reflexivity, symmetricity and transitivity:

Let A be the set consisting of all the female members of a family. The relation R defined by “aRb if a is not a sister of b”

Discuss the following relation for reflexivity, symmetricity and transitivity:

On the set of natural numbers the relation R defined by “xRy if x + 2y = 1”

Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it reflexive

Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric

Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive

Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence

Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it reflexive

Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric

Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive

Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence

Let P be the set of all triangles in a plane and R be the relation defined on P as aRb if a is similar to b. Prove that R is an equivalence relation

On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it  is reflexive

On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is symmetric

On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is transitive

On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is equivalence

Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai

On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is reflexive

On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is symmetric

On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is transitive

On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is equivalence

Let A = {a, b, c}. What is the equivalence relation of smallest cardinality on A? What is the equivalence relation of largest cardinality on A?

In the set Z of integers, define mRn if m − n is divisible by 7. Prove that R is an equivalence relation

Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer

Write the values of f at − 4, 1, −2, 7, 0 if

f(x) = `{{:(- x + 4,  "if" - ∞ < x ≤ - 3),(x + 4,  "if" - 3 < x < -2),(x^2 - x,  "if" - 2 ≤ x < 1),(x - x^2,  "if"  1 ≤ x < 7),(0,  "otherwise"):}`

Write the values of f at −3, 5, 2, −1, 0 if

f(x) = `{{:(x^2 + x - 5,  "if"  x ∈ (−∞, 0)),(x^2 + 3x - 2,  "if"  x ∈ (3, ∞)),(x^2,  "if"  x ∈ (0",", 2)),(x^2 - 3,  "otherwise"):}`

State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?

If A = {a, b, c} and f = {(a, c), (b, c), (c, b)}; (f : A → A)

State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?

If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X → X)

Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:

neither one-to-one nor onto

Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:

not one-to-one but onto

Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:

one-to-one but not onto

Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:

one-to-one and onto

Find the domain of `1/(1 - 2sinx)`

Find the largest possible domain of the real valued function f(x) = `sqrt(4 - x^2)/sqrt(x^2 - 9)`

Find the range of the function `1/(2 cos x - 1)`

Show that the relation xy = −2 is a function for a suitable domain. Find the domain and the range of the function

If f, g : R → R are defined by f(x) = |x| + x and g(x) = |x| – x find g o f and f o g

If f, g, h are real valued functions defined on R, then prove that (f + g) o h = f o h + g o h. What can you say about f o (g + h)? Justify your answer

If f : R → R is defined by f(x) = 3x − 5, prove that f is a bijection and find its inverse

The weight of the muscles of a man is a function of his body weight x and can be expressed as W(x) = 0.35x. Determine the domain of this function

The distance of an object falling is a function of time t and can be expressed as s(t) = −16t². Graph the function and determine if it is one-to-one.

The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4 m + 50 and S(m) = 0.03 m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles

A salesperson whose annual earnings can be represented by the function A(x) = 30,000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1,50,00,000 worth of merchandise

The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee

The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 − x. Express his day revenue, total cost and profit on this meal as functions of x

The formula for converting from Fahrenheit to Celsius temperatures is y = `(5x)/9 - 160/9`. Find the inverse of this function and determine whether the inverse is also a function

A simple cipher takes a number and codes it, using the function f(x) = 3x − 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x(by drawing the lines)

For the curve y = x³ given in Figure 1.67, draw
y = −x³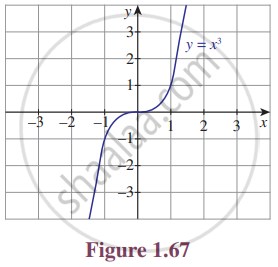 

For the curve y = x³ given in Figure 1.67, draw
y = x³ + 1 

For the curve y = x³ given in Figure 1.67, draw
y = x³ − 1 

For the curve y = x³ given in Figure 1.67, draw
y = (x + 1)³ with the same scale

For the curve y = `x^((1/3))` given in Figure 1.68, draw

y = `- x^((1/3))`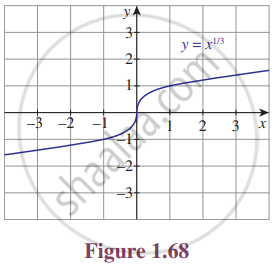

For the curve y = `x^((1/3))` given in Figure 1.68, draw

y = `x^((1/3)) + 1`

For the curve y = `x^((1/3))` given in Figure 1.68, draw

y = `x^((1/3)) - 1`

For the curve y = `x^((1/3))` given in Figure 1.68, draw

y = `(x + 1)^((1/3))`

Graph the functions f(x) = x³ and g(x) = `root(3)(x)` on the same coordinate plane. Find f o g and graph it on the plane as well. Explain your results

Write the steps to obtain the graph of the function y = 3(x − 1)² + 5 from the graph y = x² 

From the curve y = sin x, graph the function.
y = sin(− x)

From the curve y = sin x, graph the function
y = − sin(−x)

From the curve y = sin x, graph the function
y = `sin(pi/2 + x)` which is cos x

From the curve y = sin x, graph the function
y = `sin (pi/2 - x)` which is also cos x (refer trigonometry)

From the curve y = x, draw y = − x

From the curve y = x, draw y = 2x

From the curve y = x, draw y = x + 1

From the curve y = x, draw y = `1/2 x +  1`

From the curve y = x, draw 2x + y + 3 = 0

From the curve y = |x|, draw y = |x − 1| + 1

From the curve y = |x|, draw y = |x + 1| − 1

From the curve y = |x|, draw y = |x + 2| − 3

From the curve y = sin x, draw y = sin |x| (Hint: sin(−x) = − sin x)

Choose the correct alternative:

If A = {(x, y) : y = e x , x ∈ R} and B = {(x, y) : y = e^−x, x ∈ R} then n(A ∩ B) is

Choose the correct alternative:

If A = {(x, y) : y = sin x, x ∈ R} and B = {(x, y) : y = cos x, x ∈ R} then A ∩ B contains

Choose the correct alternative:

The relation R defined on a set A = {0, −1, 1, 2} by xRy if |x² + y²| ≤ 2, then which one of the following is true?

Choose the correct alternative:

If f(x) = |x − 2| + |x + 2|, x ∈ R, then

Choose the correct alternative:

Let R be the set of all real numbers. Consider the following subsets of the plane R × R: S = {(x, y) : y = x + 1 and 0 < x < 2} and T = {(x, y) : x − y is an integer} Then which of the following is true?

Choose the correct alternative:

Let A and B be subsets of the universal set N, the set of natural numbers. Then A' ∪ [(A ∩ B) ∪ B'] is

Choose the correct alternative:

The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The number of students take at least one of these two subjects, is

Choose the correct alternative:

If n((A × B) ∩ (A × C)) = 8 and n(B ∩ C) = 2, then n(A) is

Choose the correct alternative:

If n(A) = 2 and n(B ∪ C) = 3, then n[(A × B) ∪ (A × C)] is

Choose the correct alternative:

If two sets A and B have 17 elements in common, then the number of elements common to the set A × B and B × A is

Choose the correct alternative:

For non-empty sets A and B, if A ⊂ B then (A × B) ∩ (B × A) is equal to

Choose the correct alternative:

The number of relations on a set containing 3 elements is

Choose the correct alternative:

Let R be the universal relation on a set X with more than one element. Then R is

Choose the correct alternative:

Let X = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), (4, 1)}. Then R is

Choose the correct alternative:

The range of the function  `1/(1 - 2 sin x)` is

Choose the correct alternative:

The range of the function f(x) = |[x] − x|, x ∈ R is

Choose the correct alternative:

The rule f(x) = x² is a bijection if the domain and the co-domain are given by

Choose the correct alternative:

The number of constant functions from a set containing m elements to a set containing n elements is

Choose the correct alternative:

The function f : [0, 2π] → [−1, 1] defined by f(x) = sin x is

Choose the correct alternative:

If the function f : [−3, 3] → S defined by f(x) = x² is onto, then S is

Choose the correct alternative:

Let X = {1, 2, 3, 4}, Y = {a, b, c, d} and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is

Choose the correct alternative:

The inverse of f(x) = `{{:(x,  "if"  x < 1),(x^2,  "if"  1 ≤ x ≤ 4),(8sqrt(x),  "if"  x > 4):}` is

Choose the correct alternative:

Let f : R → R be defined by f(x) = 1 − |x|. Then the range of f is

Choose the correct alternative:

The function f : R → R is defined by f(x) = sin x + cos x is

Choose the correct alternative:

The function f : R → R is defined by f(x) = `((x^2 + cos x)(1 + x^4))/((x - sin x)(2x - x^3)) + "e"^(-|x|)` is