Advertisements
Advertisements
Question
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
neither one-to-one nor onto
Solution
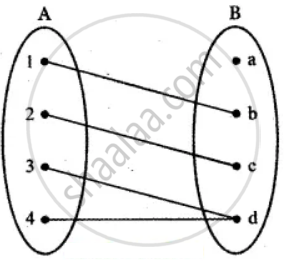
f = {(1, b), (2, c), (3, d), (4, d)}
f is a function, it not one to one and not onto.
APPEARS IN
RELATED QUESTIONS
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer
Write the values of f at −3, 5, 2, −1, 0 if
f(x) = `{{:(x^2 + x - 5, "if" x ∈ (−∞, 0)),(x^2 + 3x - 2, "if" x ∈ (3, ∞)),(x^2, "if" x ∈ (0",", 2)),(x^2 - 3, "otherwise"):}`
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
If A = {a, b, c} and f = {(a, c), (b, c), (c, b)}; (f : A → A)
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X → X)
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
one-to-one but not onto
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
one-to-one and onto
Find the domain of `1/(1 - 2sinx)`
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee
The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 − x. Express his day revenue, total cost and profit on this meal as functions of x
A simple cipher takes a number and codes it, using the function f(x) = 3x − 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x(by drawing the lines)
Choose the correct alternative:
The range of the function `1/(1 - 2 sin x)` is
Choose the correct alternative:
The function f : [0, 2π] → [−1, 1] defined by f(x) = sin x is
Choose the correct alternative:
If the function f : [−3, 3] → S defined by f(x) = x2 is onto, then S is
Choose the correct alternative:
Let X = {1, 2, 3, 4}, Y = {a, b, c, d} and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is
Choose the correct alternative:
The function f : R → R is defined by f(x) = sin x + cos x is
Choose the correct alternative:
The function f : R → R is defined by f(x) = `((x^2 + cos x)(1 + x^4))/((x - sin x)(2x - x^3)) + "e"^(-|x|)` is
