Advertisements
Advertisements
Question
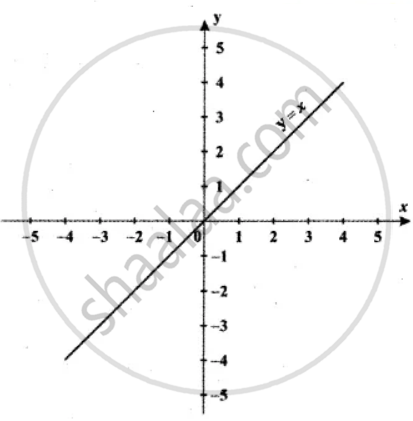
From the curve y = x, draw y = `1/2 x + 1`
Solution
| x | 0 | 1 | 2 | 3 | − 1 | − 2 | − 3 |
| y | 0 | 1 | 2 | 3 | − 1 | − 2 | − 3 |
y = `1/x + 1`
When x = 0 ⇒ y = `1/2` × 0 + 1 = 1
x = 2 ⇒ y = `1/2` × 2 + 1 = 2
x = 4 ⇒ y = `1/2` × 4 + 1 = 2 + 1 = 3
x = 6 ⇒ y = `1/2` × 6 + 1 = 3 + 1 = 4
x = – 2 ⇒ y = `1/2` × – 2 +1= – 1 + 1 = 0
x = – 4 ⇒ y = `1/2` × – 4 + 1 = – 2 + 1 = – 1
x = – 6 ⇒ y = `1/2` × – 6 + 1 = – 3 + 1 = – 2
| x | 0 | 2 | 4 | 6 | − 2 | − 4 | − 6 |
| y | 1 | 2 | 3 | 4 | 0 | − 1 | − 2 |

The graph of y = `1/2x + 1` stretches the graph y = x towards the x-axis since the multiplying factor is `1/2` which is less than 1 and shifts to the upward by 1 unit.
The graph of y = kf(x), k > 0 moves towards the x-axis if k is less than 1.
The graph of y = f(x) + d, d >0 causes the graph y = f(x) a shift to the upward by d units.
APPEARS IN
RELATED QUESTIONS
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `- x^((1/3))`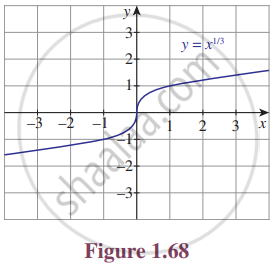
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `x^((1/3)) + 1`
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `x^((1/3)) - 1`
For the curve y = `x^((1/3))` given in Figure 1.68, draw
y = `(x + 1)^((1/3))`
Graph the functions f(x) = x3 and g(x) = `root(3)(x)` on the same coordinate plane. Find f o g and graph it on the plane as well. Explain your results
Write the steps to obtain the graph of the function y = 3(x − 1)2 + 5 from the graph y = x2
From the curve y = sin x, graph the function.
y = sin(− x)
From the curve y = sin x, graph the function
y = `sin(pi/2 + x)` which is cos x
From the curve y = sin x, graph the function
y = `sin (pi/2 - x)` which is also cos x (refer trigonometry)
From the curve y = x, draw y = − x
From the curve y = x, draw y = 2x
From the curve y = x, draw y = x + 1
From the curve y = x, draw 2x + y + 3 = 0
From the curve y = |x|, draw y = |x − 1| + 1
From the curve y = |x|, draw y = |x + 1| − 1
From the curve y = sin x, draw y = sin |x| (Hint: sin(−x) = − sin x)
