Advertisements
Advertisements
Question
Choose the correct alternative:
The rule f(x) = x2 is a bijection if the domain and the co-domain are given by
Options
R, R
R,(0, ∞)
(0, ∞), R
[0, ∞), [0, ∞)
Solution
[0, ∞), [0, ∞)
APPEARS IN
RELATED QUESTIONS
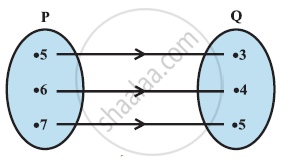
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.
Determine the domain and range of the relation R defined by
(ii) R = {(x, x3) : x is a prime number less than 10}
Let A = {a, b}. List all relations on A and find their number.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
(iii) (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f) for all (a, b), (c, d), (e, f) ∈ N × N
If A = {1, 2, 4}, B = {2, 4, 5} and C = {2, 5}, write (A − C) × (B − C).
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation defined on the set Z of integers, then write domain of R.
Let R = [(x, y) : x, y ∈ Z, y = 2x − 4]. If (a, -2) and (4, b2) ∈ R, then write the values of a and b.
R is a relation from [11, 12, 13] to [8, 10, 12] defined by y = x − 3. Then, R−1 is
If R is a relation on a finite set having n elements, then the number of relations on A is
If `(x + 1/3, y/3 - 1) = (1/2, 3/2)`, find x and y
Write the relation in the Roster Form. State its domain and range
R5 = {(x, y)/x + y = 3, x, y∈ {0, 1, 2, 3}
Answer the following:
R = {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} Check if R is reflexive
Multiple Choice Question :
The range of the relation R = {(x, x2) | x is a prime number less than 13} is ________
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric
Is the given relation a function? Give reasons for your answer.
s = {(n, n2) | n is a positive integer}
Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is ______.
A relation on the set A = {x : |x| < 3, x ∈ Z}, where Z is the set of integers is defined by R = {(x, y) : y = |x| ≠ –1}. Then the number of elements in the power set of R is ______.
