Advertisements
Advertisements
Question
The distance of an object falling is a function of time t and can be expressed as s(t) = −16t2. Graph the function and determine if it is one-to-one.
Solution
Given s(t) = –16t2
s(t1) = s(t2)
⇒ –16t12 = –16t22
⇒ t12 = t22
⇒ ± t1 = ± t2
Since s(t1) = s(t1)
⇒ 14t1 = t2
∴ The function s(t) is not one-one
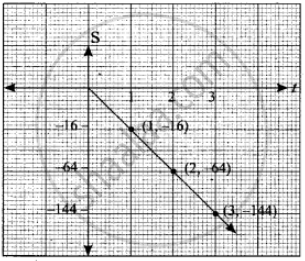
Graph of s(t) = –16t2
Take the time along x-axis and distance along y-axis.
| t | 0 | 1 | 2 | 3 |
| s(t) | 0 | – 16 | – 64 | – 144 |
APPEARS IN
RELATED QUESTIONS
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer
Write the values of f at −3, 5, 2, −1, 0 if
f(x) = `{{:(x^2 + x - 5, "if" x ∈ (−∞, 0)),(x^2 + 3x - 2, "if" x ∈ (3, ∞)),(x^2, "if" x ∈ (0",", 2)),(x^2 - 3, "otherwise"):}`
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X → X)
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
not one-to-one but onto
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A → B of the following:
one-to-one and onto
Find the largest possible domain of the real valued function f(x) = `sqrt(4 - x^2)/sqrt(x^2 - 9)`
Find the range of the function `1/(2 cos x - 1)`
Show that the relation xy = −2 is a function for a suitable domain. Find the domain and the range of the function
The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4 m + 50 and S(m) = 0.03 m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles
A salesperson whose annual earnings can be represented by the function A(x) = 30,000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1,50,00,000 worth of merchandise
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee
A simple cipher takes a number and codes it, using the function f(x) = 3x − 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x(by drawing the lines)
Choose the correct alternative:
If f(x) = |x − 2| + |x + 2|, x ∈ R, then
Choose the correct alternative:
The range of the function `1/(1 - 2 sin x)` is
Choose the correct alternative:
The number of constant functions from a set containing m elements to a set containing n elements is
Choose the correct alternative:
If the function f : [−3, 3] → S defined by f(x) = x2 is onto, then S is
Choose the correct alternative:
The function f : R → R is defined by f(x) = sin x + cos x is
Choose the correct alternative:
The function f : R → R is defined by f(x) = `((x^2 + cos x)(1 + x^4))/((x - sin x)(2x - x^3)) + "e"^(-|x|)` is
