Advertisements
Advertisements
Question
Draw a circle of radius 3 cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
Solution
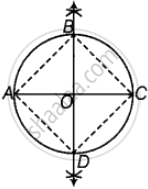
Steps of construction:
Step I: Taking centre OC = 3 cm, draw a circle.
Step II: Join A to C and draw a perpendicular bisector of AC that cuts the circumference of circle at B and D.
Step III: Join B and D.
Step IV: Thus, ABCD is a cyclic, quadrilateral.
Justification: In cyclic quadrilateral,
∠B = ∠D = 90°
∠A = ∠C = 90° ...[Angle in a semi-circle]
∠B + ∠D = 180°
And ∠A + ∠C = 180° ...[Opposite angles are supplementary]
Since, opposite angles are supplementary,
Thus, quadrilateral is a cyclic quadrilateral.
APPEARS IN
RELATED QUESTIONS
In the trapezium ABCD, the measure of ∠D is ______.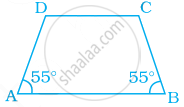
If two adjacent angles of a parallelogram are in the ratio 2 : 3, then the measure of angles are ______.
Two adjacent angles of a parallelogram are in the ratio 1:5. Then all the angles of the parallelogram are ______.
Adjacent angles of a parallelogram are ______.
Two adjacent angles of a parallelogram are in the ratio 1:3. Find its angles.
The adjacent angles of a parallelogram are (2x – 4)° and (3x – 1)°. Find the measures of all angles of the parallelogram.
In parallelogram ABCD, find ∠B, ∠C and ∠D.

